Symmedian Point

The point of concurrence of the symmedians, sometimes also called the Lemoine point (in England and France) or the Grebe point (in Germany). Equivalently, the symmedian point is the isogonal conjugate of the triangle centroid . In other words, let be the triangle centroid of a triangle , , , and the medians of , , , and the angle bisectors of angles , , , and , , and the reflections of , , and about , , and . Then is the point of concurrence of the lines , , and . According to Honsberger (1995, p. 53), the symmedian point is "one of the crown jewels of modern geometry." The symmedian point is Kimberling center .

The symmedian point has equivalent triangle center functions and

(1)

(Honsberger 1995, p. 75), or

(2)

In exact trilinear coordinates, the symmedian point is the point for which is a minimum (Honsberger 1995, pp. 75-76). A center is the triangle centroid of its own pedal triangle iff it is the symmedian point. The symmedian point is the perspectivity center of a triangle and its tangential triangle.

The following table summarizes the symmedian points for named triangles that are Kimberling centers.

triangle	Kimberling	symmedian point of given triangle
anticomplementary triangle		symmedian point of the anticomplementary triangle
circumcircle mid-arc triangle		midpoint of and
circum-medial triangle		trilinear quotient
circumnormal triangle		circumcenter
circumtangential triangle		circumcenter
contact triangle		Gergonne point
D-triangle		symmedian point
excentral triangle		mittenpunkt
first Morley triangle		first Morley center
first Yff circles triangle		intersection of lines and
inner Napoleon triangle		triangle centroid
medial triangle		complement of symmedian point
orthic triangle		symmedian point of orthic triangle
outer Napoleon triangle		triangle centroid
reference triangle		symmedian point
second Yff circles triangle		intersection of lines and
Stammler triangle		circumcenter
tangential triangle		symmedian point of the tangential triangle
second Brocard triangle		harmonic of

In the above diagram with the symmedian point,

(3)

(Honsberger 1995, p. 76).

The symmedian point lies on the Brocard axis and the Fermat axis. It lies of the Brocard circle and is the center of the cosine circle. It also lies on the Jerabek hyperbola and the Thomson cubic.

Its distances from to the sides of the triangle are

(4)

where is the Brocard angle.

Distances to some other named triangle centers are given by

			(5)
			(6)
			(7)
			(8)
			(9)

where is the triangle centroid, is the orthocenter, is the incenter, is the mittenpunkt, and is the circumcenter.

One Brocard line, triangle median, and symmedian (out of the three of each) are concurrent, with , , and meeting at a point, where is the first Brocard point and is the triangle centroid. Similarly, , , and , where is the second Brocard point, meet at a point which is the isogonal conjugate of the first (Johnson 1929, pp. 268-269).

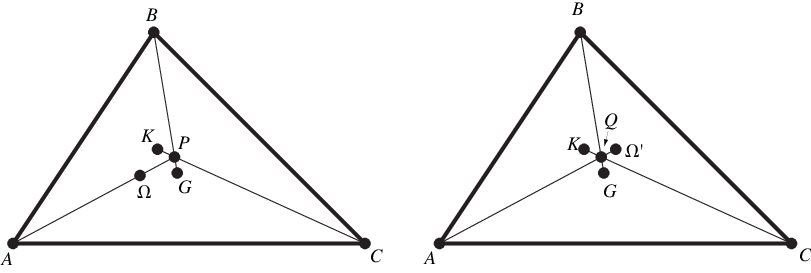
The line joining the midpoint of any side to the midpoint of the altitude on that side passes through (left figure). In particular, the symmedian point of a right triangle is the midpoint of the altitude to the hypotenuse (right figure; Honsberger 1995, p. 59). The symmedian point is the Steiner point of the first Brocard triangle.

Given a triangle , construct the triangle obtained as the intersection of the lines extended from each vertex though the symmedian point of with the circumcircle of . Then the symmedian point of is again (Honsberger 1995, p. 77).

The tangents to the circumcircle of a triangle at two of its vertices meet on the symmedian from the third vertex (Honsberger 1995, pp. 60-61). The Gergonne point of a triangle is the symmedian point of its contact triangle (Honsberger 1995, pp. 62-63). The symmedian point of a triangle is the triangle centroid of its pedal triangle. And finally, the lengths of the sides of the pedal triangle of the symmedian point are proportional to the lengths of the triangle medians of the original triangle (Honsberger 1995, p. 77).