The first Brocard point is the interior point 
(also denoted 
or 
) of a triangle 
with points labeled in counterclockwise order
for which the angles 
, 
, and 
are equal, with the unique such angle denoted 
. It is not a triangle
center, but has trilinear coordinates
 |
(1)
|
(Kimberling 1998, p. 47).
Note that extreme care is needed when consulting the literature, since reversing the order in which the points of the triangle are labeled results in exchanging the Brocard points.
The second Brocard point is the interior point 
(also denoted 
or 
) for which the angles 
, 
, and 
are equal, with the unique such angle denoted
. It is not a triangle
center, but has trilinear coordinates
 |
(2)
|
(Kimberling 1998, p. 47).
Moreover, the two angles 
are equal, and this angle is called the Brocard
angle,
 |  |  |
(3)
|
 |  |  |
(4)
|
The first two Brocard points are isogonal conjugates (Johnson 1929, p. 266). They were described by French army officer Henri Brocard in 1875, although they had previously been investigated by Jacobi and, in 1816, Crelle (Wells 1991; Honsberger 1995, p. 98). They satisfy
 |
(5)
|
where 
is the circumcenter, 
is the circumradius, and
, where 
is the circumcenter
and 
is the Brocard angle (Honsberger 1995, p. 106).
The common statement (Bernhart 1959; Wells 1991, pp. 21-22; Marshall et al. 2005) attributed to Brocard in response to an 1877 question from Edouard Lucas,
namely that if three dogs start at the vertices of a triangle and chase either their
left or right neighbor at a constant speed, the three will meet at either 
or 
, is incorrect. This can be seen by considering an isosceles triangle that is nearly collinear and
noting that two of the dogs will need to go much further than the other dog and so
can't be traveling at the same speed (cf. Peterson 2001, Nester) in order to meet
the other two at one of the points 
or 
.
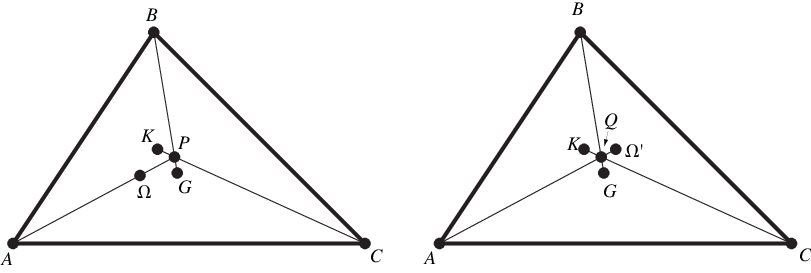
One Brocard line, triangle median, and symmedian (out of the three of each)
are concurrent, with 
, 
, and 
meeting at a point, where 
is the triangle centroid
and 
is the symmedian point. Similarly, 
, 
, and 
meet at a point which is the isogonal
conjugate of the first (Johnson 1929, pp. 268-269; Honsberger 1995, pp. 121-124).
Let 
be the circle which passes through the vertices 
and 
and is tangent to the line 
at 
, and similarly for 
and 
. Then the circles 
, 
, and 
intersect in the first
Brocard point 
.
Similarly, let 
be the circle which passes through the vertices 
and 
and is tangent to the line 
at 
, and similarly for 
and 
. Then the circles 
, 
, and 
intersect in the second
Brocard points 
(Johnson 1929, pp. 264-265; Honsberger 1995, pp. 99-100).
The pedal triangles of 
and 
are congruent, and similar
to the triangle 
(Johnson 1929, p. 269). Lengths involving the
Brocard points include
 |
(6)
|
 |
(7)
|
Extend the segments 
,
, and 
to the circumcircle
of 
to form 
,
and the segments 
,
, and 
to form 
. Then 
and 
are congruent to 
(Honsberger 1995, pp. 104-106).
The third Brocard point is related to a given triangle by the triangle center function
 |
(8)
|
(Casey 1893, Kimberling 1994) and is Kimberling center 
.
The third Brocard point 
(or 
or 
)
is collinear with the Spieker
center and the isotomic conjugate of its
triangle's incenter.
,
du plan d'un triangle 
qui se déduisent d'un point 
quelconque di plan comme les points de Brocard de déduisent
du point de Lemoine." Mathesis 6, Suppl. 3, 1-22, 1886.Marshall,
J. A.; Broucke, M. E.; and Francis, B. A. "Pursuit Formations
of Unicycles." Automata 41, 3-12, 2005.