The geometric centroid (center of mass) of the polygon vertices of a triangle
is the point
(sometimes also denoted
) which is also the intersection of the triangle's
three triangle medians (Johnson 1929, p. 249;
Wells 1991, p. 150). The point is therefore sometimes called the median point.
The centroid is always in the interior of the triangle.
It has equivalent triangle center functions
|
(1)
| |||
|
(2)
| |||
|
(3)
|
and homogeneous barycentric coordinates . It is Kimberling
center
.
The centroid satisfies
|
(4)
|
The centroid of the triangle with trilinear vertices for
, 2, 3 is given by
 |
(5)
|
(P. Moses, pers. comm., Sep. 7, 2005).
The following table summarizes the triangle centroids for named triangles that are Kimberling centers.
| triangle | Kimberling | triangle centroid |
| anticomplementary triangle | triangle centroid | |
| circumnormal triangle | circumcenter | |
| circumtangential triangle | circumcenter | |
| contact triangle | Weill point | |
| Euler triangle | midpoint of | |
| excentral triangle | centroid of the excentral triangle | |
| extouch triangle | ||
| first Brocard triangle | triangle centroid | |
| first Morley triangle | first Morley center | |
| first Neuberg triangle | triangle centroid | |
| incentral triangle | bicentric sum of pu(32) | |
| inner Napoleon triangle | triangle centroid | |
| inner Vecten triangle | triangle centroid | |
| medial triangle | triangle centroid | |
| orthic triangle | centroid of orthic triangle | |
| outer Napoleon triangle | triangle centroid | |
| outer Vecten triangle | triangle centroid | |
| reference triangle | triangle centroid | |
| second Neuberg triangle | triangle centroid | |
| Stammler triangle | circumcenter | |
| tangential triangle |
If the sides of a triangle are divided by points
,
, and
so that
|
(6)
|
then the centroid
of the triangle
is simply
, the centroid of the original triangle
(Johnson 1929, p. 250).
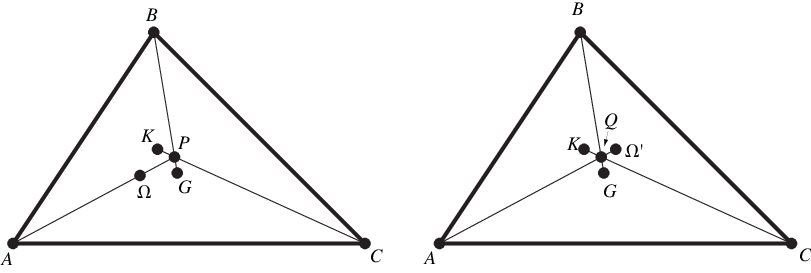
One Brocard line, triangle median, and symmedian (out of the three of each)
are concurrent, with ,
, and
meeting at a point, where
is the first brocard point
and
is the symmedian point. Similarly,
,
, and
, where
is the second Brocard
point, meet at a point which is the isogonal
conjugate of the first (Johnson 1929, pp. 268-269).
Pick an interior point . The triangles
,
, and
have equal areas iff
corresponds to the centroid. The centroid is located 2/3 of
the way from each polygon vertex to the midpoint
of the opposite side. Each median divides the triangle into two equal areas; all
the medians together divide it into six equal parts, and the lines from the centroid
to the polygon vertices divide the whole into three
equivalent triangles. In general, for any line in the
plane of a triangle
,
|
(7)
|
where ,
,
,
and
are the distances from the centroid and polygon vertices
to the line.
A triangle will balance at the centroid, and along any line passing through the centroid. The trilinear polar
of the centroid is called the Lemoine axis. The perpendiculars from the centroid are proportional
to ,
|
(8)
|
where
is the area of the triangle.
Let
be an arbitrary point, the polygon vertices be
,
,
and
,
and the centroid
.
Then
|
(9)
|
If
is the circumcenter of the triangle's centroid,
then
|
(10)
|
The distances from various named centers include
|
(11)
| |||
|
(12)
| |||
|
(13)
| |||
|
(14)
| |||
|
(15)
| |||
|
(16)
| |||
|
(17)
| |||
|
(18)
|
where
is the incenter,
is the orthocenter,
is the circumcenter,
is the symmedian
point,
is the de Longchamps point,
is the nine-point center,
is the Nagel point, and
is the Spieker center.
The centroid lies on the Euler line and Nagel line. The centroid of the perimeter of a triangle is the triangle's Spieker center (Johnson 1929, p. 249). The symmedian point of a triangle is the centroid of its pedal triangle (Honsberger 1995, pp. 72-74).
The Gergonne point , triangle centroid
, and mittenpunkt
are collinear, with
.
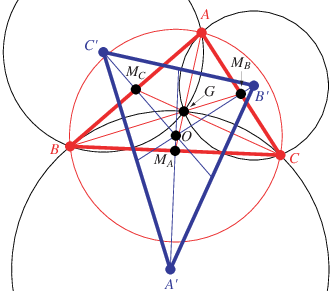
Given a triangle ,
construct circles through each pair of vertices which also pass through the triangle
centroid
.
The triangle
determined by the center of these circles then
satisfies a number of interesting properties. The first is that the circumcircle
and triangle centroid
of
are, respectively, the triangle centroid
and symmedian point
of the triangle
(Honsberger 1995, p. 77). In addition, the
triangle medians of
and
intersect in the
midpoints of the sides of
.