Binomial Coefficient

The binomial coefficient is the number of ways of picking unordered outcomes from possibilities, also known as a combination or combinatorial number. The symbols and are used to denote a binomial coefficient, and are sometimes read as " choose ."

therefore gives the number of k-subsets possible out of a set of distinct items. For example, The 2-subsets of are the six pairs , , , , , and , so . In addition, the number of lattice paths from the origin to a point ) is the binomial coefficient (Hilton and Pedersen 1991).

The value of the binomial coefficient for nonnegative integers and with is given by

(1)

(Graham et al. 1989, p.157), where denotes a factorial. Filling in values by row for , 1, ..., for increasing gives Pascal's triangle.

Writing the factorial as a gamma function allows the binomial coefficient to be generalized to noninteger arguments (including complex and ) as

(2)

The Roman coefficient (Roman 1992, Loeb 1995) is a generalization of the binomial coefficient. Whenever the binomial coefficient is defined, the Roman coefficient agrees with it. However, the Roman coefficients are defined for values for which the binomial coefficients are not.

Binomial coefficients for nonnegative integer give a polynomial in

			(3)
			(4)

where is a Pochhammer symbol. These rational coefficients are sometimes known as "generalized binomial coefficients."

Using the gamma function symmetry formula

(5)

for integer , and complex , this definition can be extended to negative integer arguments, making it continuous at all integer arguments as well as continuous for all complex arguments except for negative integer and noninteger , in which case it is infinite (Kronenburg 2011). This definition, given by

(6)

for negative integer and integer is in agreement with the binomial theorem, and with combinatorial identities with a few special exceptions (Kronenburg 2011).

The binomial coefficient is implemented in the Wolfram Language as Binomial[n, k], which follows the above convention starting in Version 8. A variation that preserves Pascal's identity

(7)

and which therefore differs in value for negative integer , is implemented in the Wolfram Language as PascalBinomial[n, k].

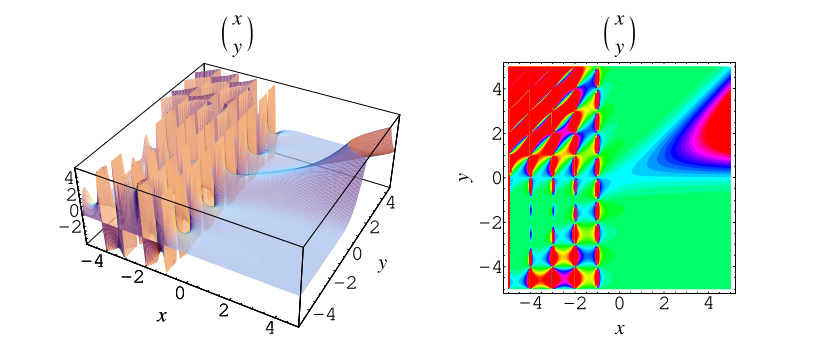
Plotting the binomial coefficient in the -plane (Fowler 1996) gives the beautiful plot shown above, which has a very complicated graph for negative and and is therefore difficult to render using standard plotting programs.

For a positive integer , the binomial theorem gives

(8)

The finite difference analog of this identity is known as the Chu-Vandermonde identity. A similar formula holds for negative integers,

(9)

There are a number of elegant binomial sums.

The binomial coefficients satisfy the identities

			(10)
			(11)
			(12)
			(13)

The product of binomial coefficients is given by

(14)

where is a hyperfactorial and is a factorial.

As shown by Kummer in 1852, if is the largest power of a prime that divides , where and are nonnegative integers, then is the number of carries that occur when is added to in base (Graham et al. 1989, Exercise 5.36, p. 245; Ribenboim 1989; Vardi 1991, p. 68). Kummer's result can also be stated in the form that the exponent of a prime dividing is given by the number of integers for which

(15)

where denotes the fractional part of . This inequality may be reduced to the study of the exponential sums , where is the Mangoldt function. Estimates of these sums are given by Jutila (1973, 1974), but recent improvements have been made by Granville and Ramare (1996).

R. W. Gosper showed that

(16)

for all primes, and conjectured that it holds only for primes. This was disproved when Skiena (1990) found it also holds for the composite number . Vardi (1991, p. 63) subsequently showed that is a solution whenever is a Wieferich prime and that if with is a solution, then so is . This allowed him to show that the only solutions for composite are 5907, , and , where 1093 and 3511 are Wieferich primes.

Consider the binomial coefficients , the first few of which are 1, 3, 10, 35, 126, ... (OEIS A001700). The generating function is

(17)

These numbers are squarefree only for , 3, 4, 6, 9, 10, 12, 36, ... (OEIS A046097), with no others known. It turns out that is divisible by 4 unless belongs to a 2-automatic set , which happens to be the set of numbers whose binary representations contain at most two 1s: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 16, 17, 18, ... (OEIS A048645). Similarly, is divisible by 9 unless belongs to a 3-automatic set , consisting of numbers for which the representation of in ternary consists entirely of 0s and 2s (except possibly for a pair of adjacent 1s). The initial elements of are 1, 2, 3, 4, 6, 7, 9, 10, 11, 12, 13, 18, 19, 21, 22, 27, ... (OEIS A051382). If is squarefree, then must belong to . It is very probable that is finite, but no proof is known. Now, squares larger than 4 and 9 might also divide , but by eliminating these two alone, the only possible for are 1, 2, 3, 4, 6, 9, 10, 12, 18, 33, 34, 36, 40, 64, 66, 192, 256, 264, 272, 513, 514, 516, 576 768, 1026, 1056, 2304, 16392, 65664, 81920, 532480, and 545259520. All of these but the last have been checked, establishing that there are no other such that is squarefree for .

Erdős showed that the binomial coefficient with is a power of an integer for the single case (Le Lionnais 1983, p. 48). Binomial coefficients are squares when is a triangular number, which occur for , 6, 35, 204, 1189, 6930, ... (OEIS A001109). These values of have the corresponding values , 9, 50, 289, 1682, 9801, ... (OEIS A052436).

The binomial coefficients are called central binomial coefficients, where is the floor function, although the subset of coefficients is sometimes also given this name. Erdős and Graham (1980, p. 71) conjectured that the central binomial coefficient is never squarefree for , and this is sometimes known as the Erdős squarefree conjecture. Sárkőzy's theorem (Sárkőzy 1985) provides a partial solution which states that the binomial coefficient is never squarefree for all sufficiently large (Vardi 1991). Granville and Ramare (1996) proved that the only squarefree values are and 4. Sander (1992) subsequently showed that are also never squarefree for sufficiently large as long as is not "too big."

For , , and distinct primes, then the function (◇) satisfies

(18)

(Vardi 1991, p. 66).

Most binomial coefficients with have a prime factor , and Lacampagne et al. (1993) conjecture that this inequality is true for all , or more strongly that any such binomial coefficient has least prime factor or with the exceptions , , , for which , 19, 23, 29 (Guy 1994, p. 84).

The binomial coefficient (mod 2) can be computed using the XOR operation XOR , making Pascal's triangle mod 2 very easy to construct.

Sondow (2005) and Sondow and Zudilin (2006) noted the inequality

(19)

for a positive integer and a real number.