The Pochhammer symbol
 |  |  |
(1)
|
 |  |  |
(2)
|
(Abramowitz and Stegun 1972, p. 256; Spanier 1987; Koepf 1998, p. 5) for 
is an unfortunate notation used
in the theory of special functions for the rising
factorial, also known as the rising factorial power (Graham et al. 1994,
p. 48) or ascending Factorial (Boros and Moll 2004, p. 16). The Pochhammer
symbol is implemented in the Wolfram Language
as Pochhammer[x,
n].
In combinatorics, the notation 
(Roman 1984, p. 5), 
(Comtet 1974, p. 6), or 
(Graham et al. 1994, p. 48) is used for
the rising factorial, while 
or 
denotes the falling
factorial (Graham et al. 1994, p. 48). Extreme caution is therefore
needed in interpreting the notations 
and 
.
The first few values of 
for nonnegative integers 
are
 |  |  |
(3)
|
 |  |  |
(4)
|
 |  |  |
(5)
|
 |  |  |
(6)
|
 |  |  |
(7)
|
(OEIS A054654).
In closed form, 
can be written
 |
(8)
|
where 
is a Stirling number of the first kind.
The Pochhammer symbol satisfies
 |
(9)
|
the dimidiation formulas
 |  |  |
(10)
|
 |  |  |
(11)
|
and the duplications formula
 |
(12)
|
(Boros and Moll 2004, p. 17).
A ratio of Pochhammer symbols is given in closed form by
 |
(13)
|
(Boros and Moll 2004, p. 17).
The derivative is given by
![d/(dx)(x)_n=(x)_n[psi_0(n+x)-psi_0(x)],](/images/equations/PochhammerSymbol/NumberedEquation5.svg) |
(14)
|
where 
is the digamma function.
Special values include
 |  |  |
(15)
|
 |  |  |
(16)
|
The Pochhammer symbol 
obeys the transformation due to Euler
 |
(17)
|
where 
is the forward difference and
 |
(18)
|
(Nørlund 1955).
The sum of 
can be done in closed form as
 |
(19)
|
for 
.
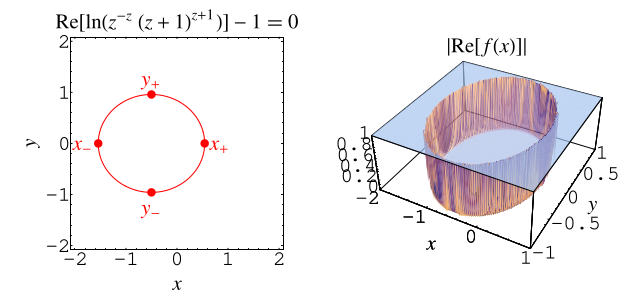
Consider the product
 |  |  |
(20)
|
 |  |  |
(21)
|
This function converges to 0, to a finite value, or diverges, depending on the value of 
.
The critical curve is given by the implicit equation
![R[-1+ln(z^(-z)(1+z)^(1+z))]=0.](/images/equations/PochhammerSymbol/NumberedEquation9.svg) |
(22)
|
Inside this curve, the function converges to 0, whereas outside it, it diverges. The maximum real value at which convergence occurs is given by 
(OEIS A090462),
and the minimum value by 
. The extremal values of 
are given by 
(OEIS A090463).
On the critical contour, 
takes on the value
![f(z)=1/2[lnz+ln(z+1)].](/images/equations/PochhammerSymbol/NumberedEquation10.svg) |
(23)
|
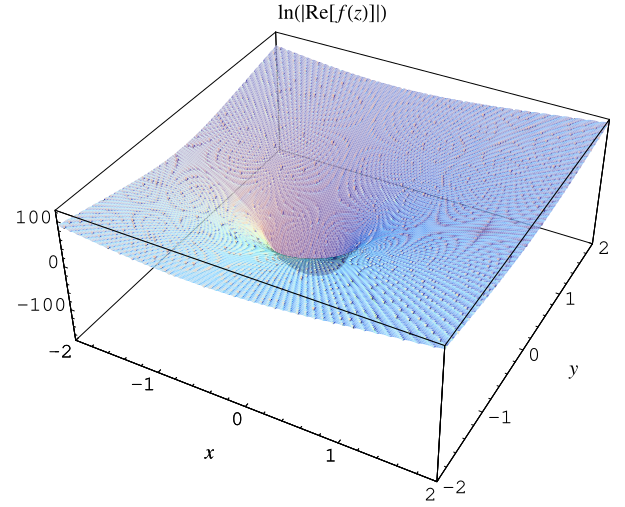
Plotting a suitably scaled version of 
with 
finite shows beautiful and subtle structures such as those
illustrated above for 
(M. Trott, pers. comm., Dec. 1, 2003).
Another beautiful visualization plots 
, as illustrated above for 
(M. Trott, pers. comm., Dec. 2, 2003).
." Ch. 18 in