|
|
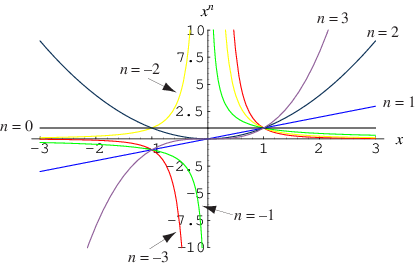
A power is an exponent to which a given quantity is raised. The expression is therefore known as "
to the
th
power." A number of powers of
are plotted above (cf. Derbyshire 2004, pp. 68 and 73).
The power may be an integer, real number, or complex number. However, the power of a real number to a non-integer power is not necessarily
itself a real number. For example, is real only for
.
A number other than 0 taken to the power 0 is defined to be 1, which follows from the limit
|
(1)
|
This fact is illustrated by the convergence of curves at in the plot above, which shows
for
,
0.4, ..., 2.0. It can also be seen more intuitively by noting that repeatedly taking
the square root of a number
gives smaller and smaller numbers that approach one from
above, while doing the same with a number between 0 and 1 gives larger and larger
numbers that approach one from below. For
square roots, the total power taken is
, which approaches 0 as
is large, giving
in the limit that
is large.
(zero to
the zeroth power) itself is undefined. The lack of a well-defined meaning for this
quantity follows from the mutually contradictory facts that
is always 1, so
should equal 1, but
is always 0 (for
), so
should equal 0. The choice of definition for
is usually defined to be indeterminate,
although defining
allows some formulas to be expressed simply (Knuth 1992; Knuth 1997, p. 57).
A number to the first power is, by definition, equal to itself, i.e.,
|
(2)
|
Similarly,
|
(3)
|
for any complex number . It is therefore impressive that Captain Kirk (William Shatner)
is able to detect one more heartbeat aboard the starship Enterprise than can
be accounted for by amplifying an auditory sensor intensified by a factor of "1
to the fourth power" in the Season 1 Star
Trek episode "Court
Martial" (1967).
The rules for combining quantities containing powers are called the exponent laws, and the process of raising a base to a given power is known as exponentiation.
The derivative of is given by
|
(4)
|
and the indefinite integral by
 |
(5)
|
The definite integral for real is known as Cavalieri's
quadrature formula and is given by
 |
(6)
|
While the simple equation
|
(7)
|
cannot be solved for
using traditional elementary functions, the
solution can be given in terms of the Lambert W-function
as
|
(8)
|
where is the natural
logarithm of
.
Similarly, the solution to
|
(9)
|
can be solved for
in terms of
using the Lambert W-function. In the special
case
, in addition to the solutions
and
, a third solution is
|
(10)
| |||
|
(11)
|
(OEIS A073084).
Special names given to various powers are listed in the following table.
Expressions of the form
are known as power towers.
The largest powers
which numbers
,
2, 3, ... can be represented in the form
are 1, 1, 1, 2, 1, 1, 1, 3, 2, 1, ... (OEIS A052409),
with corresponding values of
given by 1, 2, 3, 2, 5, 6, 7, 2, 3, 10, ... (OEIS A052410).
A double binomial sum gives the power function as follows,
 |
(12)
|
(K. MacMillan, pers. comm., Nov. 14, 2007).
The power sum of the first positive integers is given
by Faulhaber's formula,
 |
(13)
|
where is the Kronecker
delta,
is a binomial coefficient, and
is a Bernoulli number.
Let be the largest integer
that is not the sum of distinct
th powers of positive integers
(Guy 1994). The first few values for
, 3, ... are 128, 12758, 5134240, 67898771, ... (OEIS A001661).
Catalan's conjecture (now a theorem) states that 8 and 9 (
and
) are the only consecutive powers (excluding
0 and 1), i.e., the only solution to Catalan's
Diophantine problem. In addition, Hyyrő and Makowski proved that there do
not exist three consecutive powers (Ribenboim 1996).
Very few numbers of the form are prime (where composite
powers
need not be considered, since
). The only prime numbers of the form
for
and prime
correspond to
and the Mersenne primes,
i.e.,
,
,
,
.... Other numbers of the form
equal
. The
only prime numbers of the form
for
and prime
correspond to
with
,
2, 4, 6, 10, 14, 16, 20, 24, 26, ... (OEIS A005574).
Other numbers of the form
equal
.
There are no nontrivial solutions to the equation
|
(14)
|
for (Guy 1994, p. 153).