The Roman surface, also called the Steiner surface (not to be confused with the class of Steiner surfaces of which the Roman surface is a particular case), is a quartic nonorientable surface The Roman surface is one of the three possible surfaces obtained by sewing a Möbius strip to the edge of a disk. The other two are the Boy surface and cross-cap, all of which are homeomorphic to the real projective plane (Pinkall 1986).
The center point of the Roman surface is an ordinary triple point with ,
and the six endpoints of the three lines of self-intersection are singular pinch
points, also known as pinch points. The Roman
surface is essentially six cross-caps stuck together
and contains a double infinity of conics.
The Roman surface can given by the equation
|
(1)
|
Solving for
gives the pair of equations
 |
(2)
|
If the surface is rotated by about the z-axis
via the rotation matrix
![R_z(45 degrees)=1/(sqrt(2))[1 1 0; -1 1 0; 0 0 1]](/images/equations/RomanSurface/NumberedEquation3.svg) |
(3)
|
to give
![[x^'; y^'; z^']=R_z(45 degrees)[x; y; z],](/images/equations/RomanSurface/NumberedEquation4.svg) |
(4)
|
then the simple equation
|
(5)
|
results.
The Roman surface can also be generated using the general method for nonorientable surfaces using the polynomial function
|
(6)
|
(Pinkall 1986). Setting
|
(7)
| |||
|
(8)
| |||
|
(9)
|
in the former gives
|
(10)
| |||
|
(11)
| |||
|
(12)
|
for
and
.
This gives algebraic equation
|
(13)
|
corresponding to
in the general equation above. The coefficients of the first
fundamental form and second fundamental
form are slightly complicated, as are the Gaussian and mean curvatures. The volume enclosed is given by
|
(14)
|
and its moment of inertia tensor by
![I=[1/(10)Ma^2 0 0; 0 1/(10)Ma^2 0; 0 0 1/(10)Ma^2].](/images/equations/RomanSurface/NumberedEquation9.svg) |
(15)
|
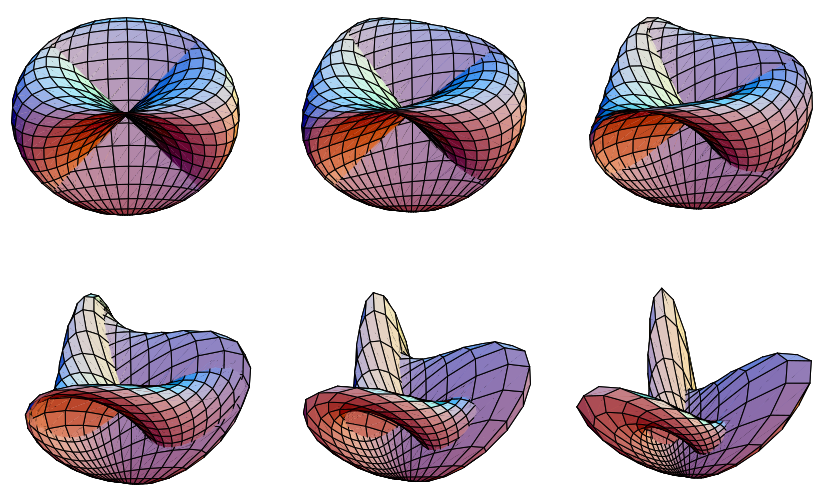
A homotopy (smooth deformation) between the Roman surface and Boy surface is given by the equations
 |
(16)
| ||
 |
(17)
| ||
|
(18)
|
for
and
as
varies from 0 to 1.
corresponds to the Roman surface and
to the Boy surface.