Möbius Strip

The Möbius strip, also called the twisted cylinder (Henle 1994, p. 110), is a one-sided nonorientable surface obtained by cutting a closed band into a single strip, giving one of the two ends thus produced a half twist, and then reattaching the two ends (right figure; Gray 1997, pp. 322-323). The strip bearing his name was invented by Möbius in 1858, although it was independently discovered by Listing, who published it, while Möbius did not (Derbyshire 2004, p. 381). Like the cylinder, it is not a true surface, but rather a surface with boundary (Henle 1994, p. 110).

The Möbius strip has Euler characteristic (Dodson and Parker 1997, p. 125).

According to Madachy (1979), the B. F. Goodrich Company patented a conveyor belt in the form of a Möbius strip which lasts twice as long as conventional belts. M. C. Escher was fond of portraying Möbius strips, and they appear in his woodcuts "Möbius Strip I" and "Möbius Strip II (Red Ants)" (Bool et al. 1982, p. 324; Forty 2003, Plate 70).

A Möbius strip of half-width with midcircle of radius and at height can be represented parametrically by

			(1)
			(2)
			(3)

for and . In this parametrization, the Möbius strip is therefore a cubic surface with equation

(4)

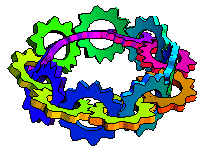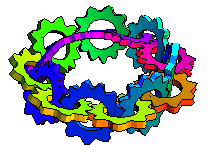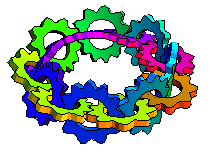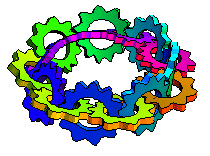
The illustration above shows interlocked turning gears along the length of a Möbius strip (M. Trott, pers. comm., 2001).

The coefficients of the first fundamental form for this surface are

			(5)
			(6)
			(7)

the second fundamental form coefficients are

			(8)
			(9)
			(10)

the area element is

(11)

and the Gaussian and mean curvatures are

		$-(4R^2)/({4R^2+3s^2+2s[4Rcos(1/2t)+scost]}^2)$	(12)
		$(2[2(R^2+s^2)+4Rscos(1/2t)+s^2cost]sin(1/2t))/({4R^2+3s^2+2s[4Rcos(1/2t)+scost]}^2).$	(13)

The perimeter of the Möbius strip is given by integrating the complicated function

$ds=sqrt(x^('2)+y^('2)) =[1/(16)w^4cos^4(1/2t)+{[R+wcos(1/2t)]cost-1/2wsin(1/2t)sint}^4+{Rsint+1/4w[sin(1/2t)+3sin(3/2t)]}^4]^(1/2)$

(14)

from 0 to , which can unfortunately not be done in closed form. Note that although the surface closes at , this corresponds to the bottom edge connecting with the top edge, as illustrated above, so an additional must be traversed to comprise the entire arc length of the bounding edge.

Cutting a Möbius strip, giving it extra twists, and reconnecting the ends produces unexpected figures called paradromic rings (Listing and Tait 1847, Ball and Coxeter 1987) which are summarized in the table below.

half-twists	cuts	divs.	result
1	1	2	1 band, length 2
1	1	3	1 band, length 2
			1 Möbius strip, length 1
1	2	4	2 bands, length 2
1	2	5	2 bands, length 2
			1 Möbius strip, length 1
1	3	6	3 bands, length 2
1	3	7	3 bands, length 2
			1 Möbius strip, length 1
2	1	2	2 bands, length 1
2	2	3	3 bands, length 1
2	3	4	4 bands, length 1

A torus can be cut into a Möbius strip with an even number of half-twists, and a Klein bottle can be cut in half along its length to make two Möbius strips. In addition, two strips on top of each other, each with a half-twist, give a single strip with four twists when disentangled.

The topological result of attaching a Möbius strip to a disk along its boundary is a real projective plane, which cannot be embedded in . However, there are three surfaces that are representations of the projective plane in with self-intersections, namely the Boy surface, cross-cap, and Roman surface.

Any set of regions on the Möbius strip can be colored using only six colors, as illustrated in Tietze's graph above.

Möbius Strip

Wolfram Web Resources