A group action of a group 
on a set 
is a map 
such that the
following conditions hold for all elements 
.
1. 
where 
is the identity element
of 
.
2. 
for
all 
.
In this case, 
is called a transformation group,
is called a 
-set, and 
is called the group action.
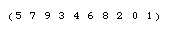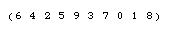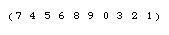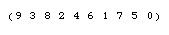
In a group action, a group permutes the elements of 
. The identity
element does nothing, while a composition of
group actions corresponds to the action of the composition.
For example, as illustrated above, the symmetric group 
acts on the digits 0 to 9 by permutations.
For a given 
,
the set 
, where the group action moves 
, is called the group orbit
of 
. The subgroup
which fixes 
is the isotropy group of 
.
For example, the group ![Z_2={[0],[1]}](/images/equations/GroupAction/Inline22.svg)
acts on the real numbers
by multiplication by 
. The identity element
leaves everything fixed, while ![[1]](/images/equations/GroupAction/Inline24.svg)
sends 
to 
.
Note that ![[1]·[1]=[0]](/images/equations/GroupAction/Inline27.svg)
,
which corresponds to 
.
For 
, the group
orbit of 
is 
, and the isotropy
group is the trivial group, ![{[0]}](/images/equations/GroupAction/Inline32.svg)
. The only group fixed
point of this action is 
.
In a group representation, a group acts by invertible linear
transformations of a vector space 
. In fact, a group representation
is a group homomorphism from 
to 
,
the general linear group of 
. Some groups are described in a
group representation, such as the special
linear group, although they may have different group
representations.
An important example is the group action of the Galois group on the roots of a polynomial. However, there are numerous examples and applications of group actions in many branches of mathematics, including algebra, topology, geometry, number theory, and analysis, as well as the sciences, including chemistry and physics.
