The likelihood of a simple graph is defined by starting with the set . The following procedure is then iterated to produce
a set of graphs
of order
.
At step
,
randomly pick an integer
from the set
. Now randomly pick one of graphs in
(keeping the probability that it was constructed in
step
)
and from it add a new vertex that is connected to all of
randomly selected of its existing vertices. Now merge any
isomorphic graphs produced by this procedure by totalling the their probabilities.
The likelihood of a graph
on
vertices is then defined as the probability that
appears in
.
The th
iteration of this procedure produces every possible graph on
nodes,. The results for graphs on
to 4 nodes are illustrated above. Likelihoods for all simple
graphs of size up to 10 nodes have been computed by E. Weisstein (Dec. 23,
2013).
, where
is the graph complement
of
.
and
are therefore co-likely.
Since the values are probabilities, the sum of likelihoods over all -node graphs is 1 and individual likelihoods satisfy
|
(1)
|
with
holding only for
.
also satisfies the stronger inequality
 |
(2)
|
where
is the order of the automorphism group of
(Banerji et al. 2014).
The following table summarizes the likelihoods for members of a number of special classes.
| graph | OEIS | values |
| Andrásfai graph | A000000/A000000 | |
| antiprism graph | A000000/A000000 | 13/21600, 1909/2540160000, ... |
| barbell graph | A000000/A000000 | 97/129600, 79/282240000, ... |
| cocktail
party graph | A000000/A000000 | 1/2, 1/36, 13/21600, 11/1587600, ... |
| complete graph | A000000/A000000 | 1, 1/2, 1/6, 1/24, 1/120, 1/720, ... |
| crown graph | A000000/A000000 | 29/64800, 11/40642560, ... |
| cycle graph | A000000/A000000 | 1/2, 1/270, 1909/2540160000, ... |
| empty graph | A000000/A000000 | 1, 1/2, 1/6, 1/24, 1/120, 1/720, ... |
| hypercube
graph | A000000/A000000 | 1, 1/2, 1/36, 11/40642560, ... |
| ladder graph | A000000/A000000 | 1/2, 1/36, 61/43200, 20299/2540160000, ... |
| ladder rung graph | A000000/A000000 | 1/2, 1/36, 13/21600, 11/1587600, ... |
| Möbius
ladder | A000000/A000000 | 23/259200, 1909/2540160000, ... |
| path graph | A000000/A000000 | 1, 1/2, 1/3, 1/9, 29/1080, 2/405, 2509/3402000, 1889/20412000, ... |
| prism graph | A000000/A000000 | 29/64800, 11/40642560, ... |
| star graph | A000000/A000000 | 1, 1/2, 1/3, 5/72, 17/1440, 77/43200, 437/1814400 |
| sun graph | A000000/A000000 | 59/25920, 101/9072000, ... |
| triangular graph | A000000/A000000 | 1, 1/6, 13/21600, ... |
| wheel graph | A000000/A000000 | 1/24, 13/720, 203/129600, 2393/18144000, ... |
Classes with known closed form values include
|
(3)
| |||
|
(4)
| |||
 |
(5)
| ||
|
(6)
| |||
 |
(7)
|
where
is a complete graph,
is an empty graph,
is a star
graph,
is a ladder rung graph,
is a factorial, and
is a subfactorial. In addition,
there is a relationship between
for a cycle graph and
for a path
graph given by
|
(8)
|
(Banerji et al. 2014).
In general, a graph on vertices with
isolated edges has likelihood
 |
(9)
| ||
 |
(10)
|
giving special cases
|
(11)
| |||
|
(12)
|
where
is a harmonic number.
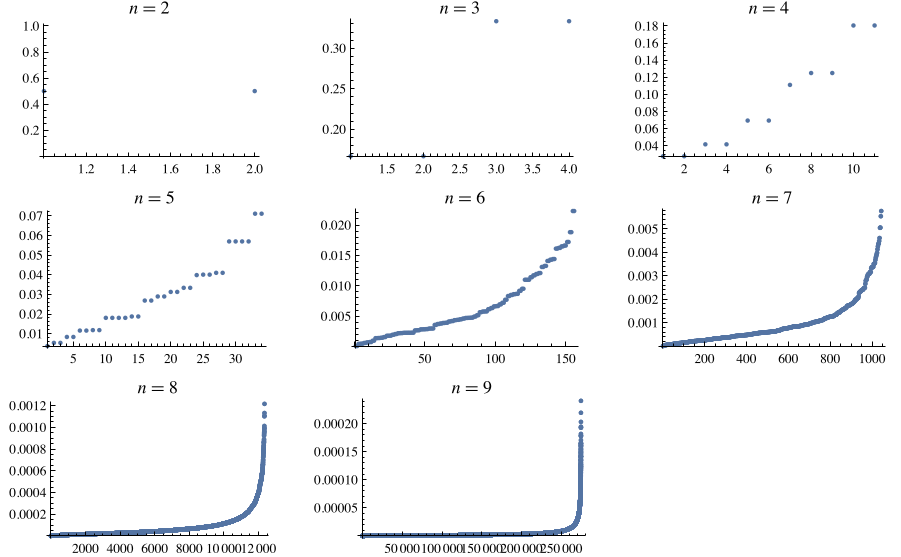
Values of
for
-nodes
graphs are plotted above.
For all values of
except
,
3, and 5 (for which the minima occur for
,
, and
, respectively), the minimum value of
occurs for the complete
bipartite graph
and its graph complement. The minimum values
of
for
,
2, ... are 1, 1/2, 1/6, 1/36, 1/270, 23/259200, 319/54432000, 319/15240960000, ...
(OEIS A234234 and A234235).
The situation for maximum as a function of
is less clear, with maxima occurring for
, 2, ... for
,
,
, paw graph, dart
graph, ... and their complements. The corresponding maximum values are 1, 1/2,
1/3, 13/72, 307/4320, 1927/86400, 39211/6804000, 27797639/22861440000, ... (OEIS
A234236 and A234237).