Augmentation is the dual operation of truncation which replaces the faces of a polyhedron with pyramids
of height
(where
may be positive, zero, or negative) having the face as the base (Cromwell 1997, p. 124
and 195-197). The operation is sometimes also called accretion, akisation (since
it transforms a regular polygon to an
-akis polyhedron, i.e., quadruples the number of faces), capping,
or cumulation.
B. Grünbaum used the terms elevatum and invaginatum for positive-height (outward-pointing) and negative-height (inward-pointing), respectively, pyramids used in augmentation.
The term "augmented" is also sometimes used in the more general context of affixing one polyhedral cap over the face of a base solid. An example is the Johnson solid called the augmented truncated cube, for which the affixed shape is a square cupola--not a pyramid.
Augmentation is implemented under the misnomer Stellate[poly, ratio] in the Wolfram Language package PolyhedronOperations` and is implemented in the Wolfram Language as AugmentedPolyhedron[poly].
Mineralogists give the following special names to augmented forms of regular solids (Berry and Mason 1959, pp. 124 and 127).
| solid | name of augmentation | mineralogical name |
| cube | tetrakis hexahedron | tetrahexahedron |
| octahedron | small triakis octahedron | trisoctahedron |
| tetrahedron | triakis tetrahedron | tristetrahedron |
Augmentation with
gives a triangulated version of the original solid. Augmentation series from negative
to positive augmentation heights are illustrated below for the Platonic
solids.
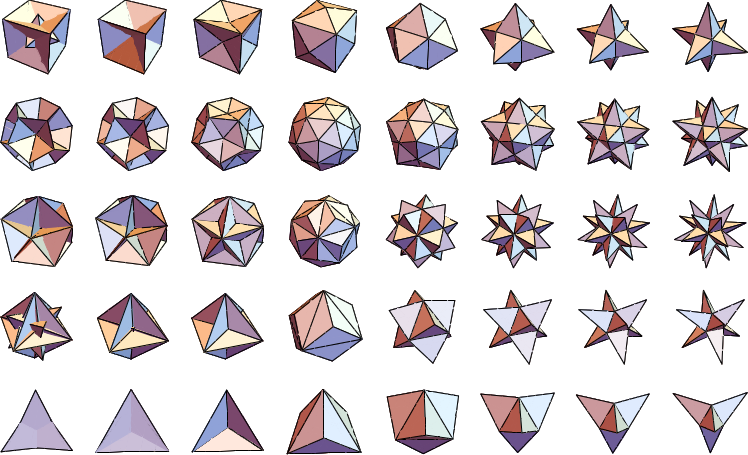
The figure and table below give special solids formed by augmentation of given heights on Platonic solids with unit edge lengths.

|

|

|

|
The top images above show an origami augmented tetrahedron and augmented dodecahedron. They are built using triangle edge modules and constructed
in a manner similar to other solids described by Gurkewitz and Arnstein (1995, p. 53).
The bottom left figure shows an inwardly augmented dodecahedron (Fusè 1990,
pp. 126-129) corresponding to icosahedron
stellation
(number 26) in Coxeter et al. (1999, pp. 43 and 64), while the right
figure shows an augmented icosahedron constructed by E. W. Weisstein (Kasahara
and Takahama 1987, p. 45).