The pentakis dodecahedron is the 60-faced dual polyhedron of the truncated icosahedron (Holden 1971,
p. 55). It can be constructed by augmentation
of a unit edge-length dodecahedron by a pyramid
with height .
It is illustrated above together with a wireframe version and a net
that can be used for its construction.
It is Wenninger dual .
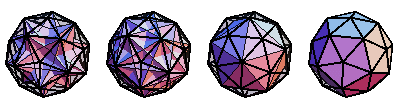
A tetrahedron 10-compound, cube 5-compound, icosahedron, and dodecahedron can be inscribed in the vertices of the pentakis dodecahedron (E. Weisstein, Dec. 25-27, 2009).
The pentakis dodecahedron is he convex hull of the small triambic icosahedron hull.
Taking the dual of a truncated icosahedron with unit edge lengths gives a pentakis dodecahedron with edge lengths
|
(1)
| |||
|
(2)
|
Normalizing so that , the surface area and
volume are
|
(3)
| |||
|
(4)
|
