The (first) rhombic dodecahedron is the dual polyhedron of the cuboctahedron (Holden 1971, p. 55). It is sometimes also called the rhomboidal dodecahedron (Cotton 1990), and the "first" may be included when needed to distinguish it from the Bilinski dodecahedron (Bilinski 1960, Chilton and Coxeter 1963). It is illustrated above together with a wireframe version and a net that can be used for its construction.
It is Wenninger dual .
The rhombic dodecahedron is implemented in the Wolfram Language as PolyhedronData["RhombicDodecahedron"].
A rhombic dodecahedron appears in the upper right as one of the polyhedral "stars" in M. C. Escher's 1948 wood engraving "Stars" (Forty 2003, Plate 43).
The 14 vertices of the rhombic dodecahedron are joined by 12 rhombi of the dimensions shown in the figure below, where
|
(1)
| |||
|
(2)
| |||
|
(3)
| |||
|
(4)
| |||
|
(5)
|
|
|
|
|
The rhombic dodecahedron can be built up by a placing six cubes on the faces of a seventh, in the configuration of a metal "jack" (left figure). Joining the centers of the outer cubes with the vertices of the central cube then gives the rhombic dodecahedron (middle figure). Affixing a square pyramid of height 1/2 on each face of a cube having unit edge length results in a rhombic dodecahedron (right figure; Brückner 1900, p. 130; Steinhaus 1999, p. 185).
Connecting the long diagonals of a rhombic dodecahedron (shown in blue above) gives the edges of an octahedron, while the short diagonals gives the edges of a cube (red).
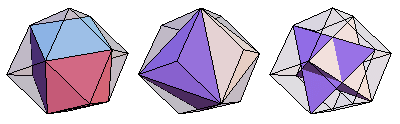
More specifically, a cube, octahedron, and stella octangula can be inscribed in the vertices of a rhombic dodecahedron (E. Weisstein, Dec. 25, 2009).
The rhombic dodecahedron is the convex hull of the cube-octahedron compound and the first cuboctahedron stellation.
If the rhombic dodecahedron is hinged into six square pyramids along three consecutive face diagonals, the resulting model can be folded into a cube (Wells 1991). One possible construction for the rhombic dodecahedron is known as the Bauspiel. It can also be constructed by augmentation of a unit edge-length cube by a pyramid with height 1/2.
The rhombic dodecahedron is a zonohedron and a space-filling polyhedron (Steinhaus 1999,
p. 185). The vertices are given by (,
,
), (
, 0, 0), (0,
, 0), (0, 0,
).
|
|
|
The edges of the cube-octahedron compound intersecting in the points plotted above are the diagonals of rhombi (left figure), and the 12 rhombi form a rhombic dodecahedron (center figure; Ball and Coxeter 1987). The cuboctahedron can be inscribed in the rhombic dodecahedron (right figure; Steinhaus 1999, p. 206).
There are three stellations of the rhombic dodecahedron.

The rhombic dodecahedron can be built using a Haűy construction. The Haűy rhombic dodecahedral numbers
|
(6)
|
give a method for calculating the volume of the rhombic dodecahedron,
 |
(7)
| ||
|
(8)
|
(Steinhaus 1999). The surface area of a rhombic dodecahedron with unit edge length is
|
(9)
|
and its inertia tensor is
![I=[1/3Ma^2 0 0; 0 1/3Ma^2 0; 0 0 1/3Ma^2].](/images/equations/RhombicDodecahedron/NumberedEquation3.svg) |
(10)
|
