The small triambic icosahedron is the dual polyhedron of the small ditrigonal icosidodecahedron with Maeder index 30 (Maeder 1997), Weinninger index 70 (Wenninger 1971, p. 106-107), Coxeter index 39 (Coxeter et al. 1954), and Har'El index 35 (Har'El 1993). Note that while Wenninger (1989, p. 49) calls this solid the triakis octahedron, this term more commonly used for the dual of one of the Archimedean solids.
The small triambic icosahedron is implemented in the Wolfram Language as PolyhedronData["SmallTriambicIcosahedron"].
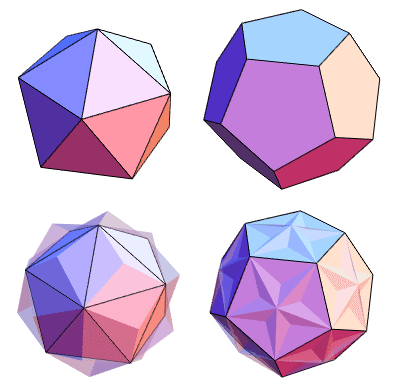
It is illustrated above together with its dual.
The small triambic icosahedron consists of 20 equilateral irregular hexagons with alternating angles
|
(1)
| |||
|
(2)
| |||
|
(3)
| |||
 |
(4)
| ||
|
(5)
|
It has Dehn invariant
|
(6)
| |||
 |
(7)
|
where the first expression uses the basis of Conway et al. (1999).
The convex hull of the small ditrigonal icosidodecahedron is a regular dodecahedron whose dual is the icosahedron, so the dual of the small ditrigonal icosidodecahedron (i.e., the small triambic icosahedron) is one of the icosahedron stellations (Wenninger 1983, p. 42). In fact, it is the second icosahedron stellation in the enumeration of Maeder (1994).
Its skeleton is the rhombic triacontahedral graph.
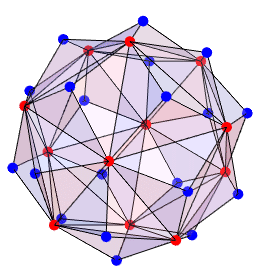
The hull of the small triambic icosahedron can be constructed by augmentation of a unit edge-length icosahedron by a pyramid with
height ,
giving a solid with edge lengths
and 1.
The small triambic icosahedron hull has 32 vertices, 90 edges, and 70 faces. Its vertices are arranged in two concentric groups of 12 (indicated in red in the above illustration) and 20 (blue).
For a small triambic icosahedron hull with edge lengths
|
(8)
| |||
|
(9)
|
the vertices determine a regular icosahedron and regular dodecahedron with circumradii
|
(10)
| |||
|
(11)
|
respectively.
The solid in the right figure is the dodecahedron-small triambic icosahedron compound.
The surface area and volume of the small triambic icosahedron hull are
|
(12)
| |||
|
(13)
|
The solid small triambic icosahedron has moment of inertia tensor
![I=[1/(300)(53+19sqrt(5))Ma^2 0 0; 0 1/(300)(53+19sqrt(5))Ma^2 0; 0 0 1/(300)(53+19sqrt(5))Ma^2]](/images/equations/SmallTriambicIcosahedron/NumberedEquation1.svg) |
(14)
|
for uniform density solid of mass .