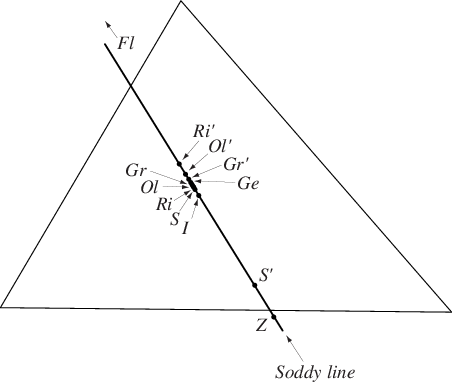
The triangle line that passes through the inner and outer Soddy centers and
.
The Soddy line is central line and has trilinear equation
It passes through Kimberling centers for
(incenter
), 7 (Gergonne point Ge),
20 (de Longchamps point
), 77, 170, 175 (outer Soddy
center
),
176 (inner Soddy center
), 269, 279, 347, 390, 481 (first
Eppstein point), 482 (second Eppstein point),
962 (the Longuet-Higgins point), 990, 991, 1042, 1044, 1323 (Fletcher
point Fl), 1371 (inner Rigby point
), 1372 (outer Rigby
point
),
1373 (inner Griffiths point
), 1374 (outer Griffiths point
), 1442, 1443, 1448, 1458, 1721, 1742,
1770, 2263, 2293, 2951, 3000, 3007, 3010, 3012, and 3019.
The points ,
,
, and Ge form a harmonic
range on the Soddy line (Vandeghen 1964, Oldknow 1996). There are a total of
22 harmonic ranges for sets of four points out
of these 10 (Oldknow 1996). The Soddy line intersects
the Euler line in the de
Longchamps point and the Gergonne line in the
Fletcher point. Furthermore, the Soddy line and
Gergonne line are perpendicular
(Oldknow 1996).
The Soddy line is the radical line of the GEOS circle and Euler-Gergonne-Soddy circle.
The angle between the orthic axis and Gergonne line is equal to that between the Euler line and the Soddy line (F. Jackson, pers. comm., Nov. 2, 2005).