The Gergonne line is Oldknow's (1996) term for the perspectrix of a contact triangle and its reference
triangle
.
It is determined by the Nobbs points
,
,
and
.
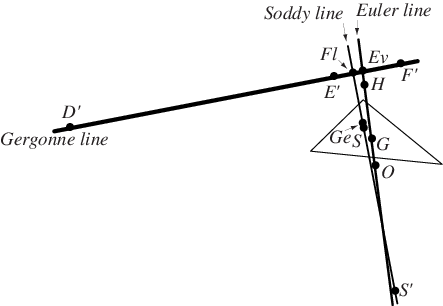
In addition to the Nobbs points, the Fletcher point (intersection with the Soddy line) and Evans point (intersection with the Euler line) also lie on the Gergonne line. Furthermore, the Soddy line and Gergonne line are perpendicular (Oldknow 1996).
The Gergonne line is central line and has trilinear equation
where
is the semiperimeter of
. It passes through Kimberling centers
for
, 514, 650, 665, 1323 (Fletcher
point), and 1375 (Evans point), 1465, 1638, 3002,
3004, 3008, and 3015.
The Gergonne line is the perspectrix of the contact triangle and reference triangle, as well as the excentral triangle and medial triangle.
It is the radical line of the coaxal system (Bevan circle, excircles radical circle, polar circle) and (incircle, inner Soddy circle, outer Soddy circle).
The angle between the orthic axis and Gergonne line is equal to that between the Euler line and the Soddy line (F. Jackson, pers. comm., Nov. 2, 2005).