The word "rigid" has two different meaning when applied to a graph. Firstly, a rigid graph may refer to a graph having a graph automorphism group containing a single element. In this work, such a graph is instead referred to using the more common term "identity graph" (e.g., Albertson and Collins 1996).
The more common meaning of rigidity considers a graph's resistance to deformation, where graph edges are commonly taken as rigid straight bars or rods that are connected
to incident vertices via flexible hinges. (Other edge elements such as cables and
struts are sometimes also considered.) Rigidity of a framework , i.e., a structure with vertex coordinates
and underlying graph
having vertex set
and edge set
, can be thought of in two equivalent
ways: infinitesimal rigidity (which considers infinitesimal displacements corresponding
to velocity vectors) and static rigidity (which considers forces and loads on the
structure).
A framework consisting of bars is said to be (infinitesimally) rigid iff continuous motion of the points of the configuration
maintaining the bar constraints comes from a family of motions of all Euclidean
space which are distance-preserving. This is equivalent to the condition that
there exists an
such that every framework
which is equivalent to
and satisfies
for all
is congruent to the framework
.
A framework
is infinitesimally rigid iff the rank of its rigidity
matrix
satisfies
where
is the vertex count (Grasegger 2023).
Call a framework
a generic realization of
if the rigidity matrix
is equal to the rigidity matroid
. This occurs when the coordinates of all points
are algebraically independent over the field of rationals
. A graph (as an abstract object with
no explicit embedding) is said to be rigid iff there is a
generic realization for which the framework is generically rigid. Similarly, a graph
is said to be (generically)
-rigid if, for almost all (i.e., an open dense set of) configurations
of
, the framework
is rigid in
.
A graph that is not rigid is said to be flexible (Maehara 1992).
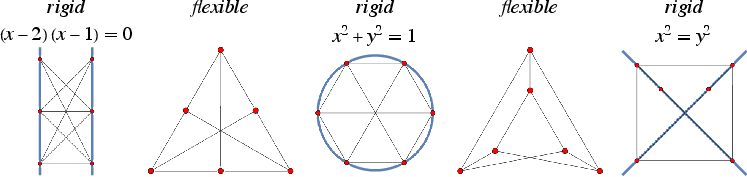
Any embeding of the triangle graph is rigid, while any embedding of the square
graph
is flexible.
A flexible graph cannot have a rigid embedding. However, in general, a rigid graph may have both rigid and flexible embeddings. For
example, an embedding of the utility graph in the plane is rigid unless its
six vertices lie on a conic (Bolker and Roth 1980,
Maehara 1992), some examples of which are illustrated above.
Cauchy (1813) proved the rigidity theorem, one of the first results in rigidity theory. Although rigidity problems were of immense interest to engineers, intensive mathematical study of these types of problems has occurred only relatively recently (Connelly 1993, Graver et al. 1993).