Parabola -- from Wolfram MathWorld

Parabola

A parabola (plural "parabolas"; Gray 1997, p. 45) is the set of all points in the plane equidistant from a given line (the conic section directrix) and a given point not on the line (the focus). The focal parameter (i.e., the distance between the directrix and focus) is therefore given by , where is the distance from the vertex to the directrix or focus. The surface of revolution obtained by rotating a parabola about its axis of symmetry is called a paraboloid.

The parabola was studied by Menaechmus in an attempt to achieve cube duplication. Menaechmus solved the problem by finding the intersection of the two parabolas and . Euclid wrote about the parabola, and it was given its present name by Apollonius. Pascal considered the parabola as a projection of a circle, and Galileo showed that projectiles falling under uniform gravity follow parabolic paths. Gregory and Newton considered the catacaustic properties of a parabola that bring parallel rays of light to a focus (MacTutor Archive), as illustrated above.

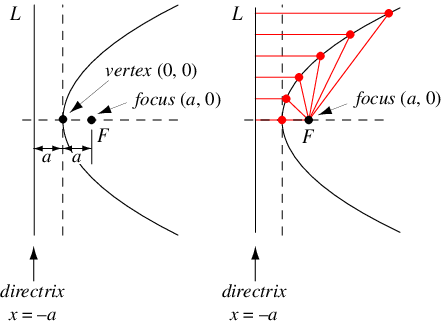
For a parabola opening to the right with vertex at (0, 0), the equation in Cartesian coordinates is

(1)

(2)

(3)

(4)

The quantity is known as the latus rectum. If the vertex is at instead of (0, 0), the equation of the parabola is

(5)

If the parabola instead opens upwards, its equation is

(6)

Three points uniquely determine one parabola with directrix parallel to the -axis and one with directrix parallel to the -axis. If these parabolas pass through the three points , , and , they are given by equations

|x^2 x y 1; x_1^2 x_1 y_1 1; x_2^2 x_2 y_2 1; x_3^2 x_3 y_3 1|=0

(7)

and

|y^2 x y 1; y_1^2 x_1 y_1 1; y_2^2 x_2 y_2 1; y_3^2 x_3 y_3 1|=0.

(8)

In polar coordinates, the equation of a parabola with parameter and center (0, 0) is given by

(9)

(left figure). The equivalence with the Cartesian form can be seen by setting up a coordinate system and plugging in and to obtain

(10)

Expanding and collecting terms,

(11)

so solving for gives (◇). A set of confocal parabolas is shown in the figure on the right.

In pedal coordinates with the pedal point at the focus, the equation is

(12)

The parabola can be written parametrically as

			(13)
			(14)

			(15)
			(16)

A segment of a parabola is a Lissajous curve.

A parabola may be generated as the envelope of two concurrent line segments by connecting opposite points on the two lines (Wells 1991).

In the above figure, the lines , , and are tangent to the parabola at points , , and , respectively. Then (Wells 1991). Moreover, the circumcircle of passes through the focus (Honsberger 1995, p. 47). In addition, the foot of the perpendicular to a tangent to a parabola from the focus always lies on the tangent at the vertex (Honsberger 1995, p. 48).

Given an arbitrary point located "outside" a parabola, the tangent or tangents to the parabola through can be constructed by drawing the circle having as a diameter, where is the focus. Then locate the points and at which the circle cuts the vertical tangent through . The points and (which can collapse to a single point in the degenerate case) are then the points of tangency of the lines and and the parabola (Wells 1991).

The curvature, arc length, and tangential angle are

			(17)
			(18)
			(19)

The tangent vector of the parabola is

			(20)
			(21)

The plots below show the normal and tangent vectors to a parabola.

REFERENCES:

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 198 and 222-223, 1987.

Casey, J. "The Parabola." Ch. 5 in A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 173-200, 1893.

Coxeter, H. S. M. "Conics." §8.4 in Introduction to Geometry, 2nd ed. New York: Wiley, pp. 115-119, 1969.

Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

Hilbert, D. and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea, p. 4, 1999.

Honsberger, R. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer., pp. 47-48, 1995.

Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 67-72, 1972.

Lockwood, E. H. "The Parabola." Ch. 1 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 2-12, 1967.

Loomis, E. S. "The Parabola." §2.5 in The Pythagorean Proposition: Its Demonstrations Analyzed and Classified and Bibliography of Sources for Data of the Four Kinds of "Proofs," 2nd ed. Reston, VA: National Council of Teachers of Mathematics, pp. 25-28, 1968.

MacTutor History of Mathematics Archive. "Parabola." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Parabola.html.

Pappas, T. "The Parabolic Ceiling of the Capitol." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 22-23, 1989.

Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 169-172, 1991.

Yates, R. C. "Conics." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 36-56, 1952.

CITE THIS AS:

Weisstein, Eric W. "Parabola." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Parabola.html