
|
|
|
The equation of the curve of intersection of a torus with a plane perpendicular to both the midplane of the torus and to the plane . (The general intersection of a torus
with a plane is called a toric section). Let the
tube of a torus have radius
, let its midplane lie in the
plane, and let the center of the tube lie at a distance
from the origin. Now cut the torus with
the plane
.
The equation of the torus with
gives the equation
|
(1)
|
|
(2)
|
|
(3)
|
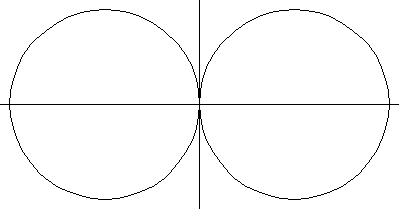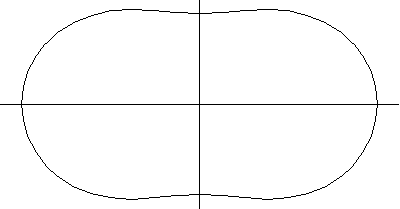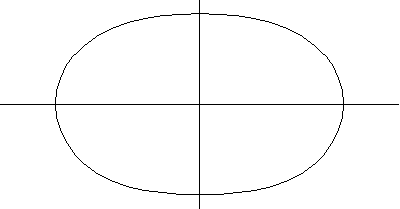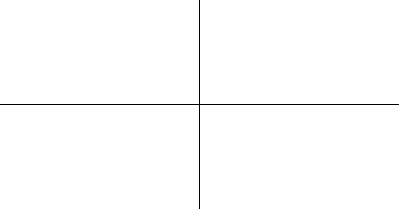
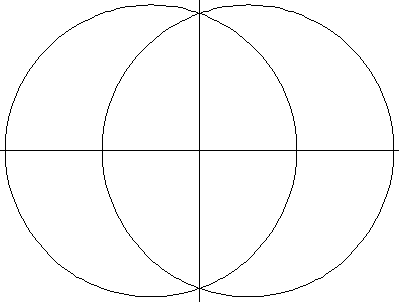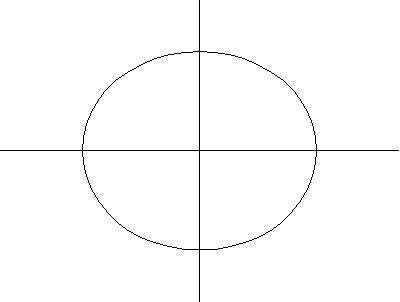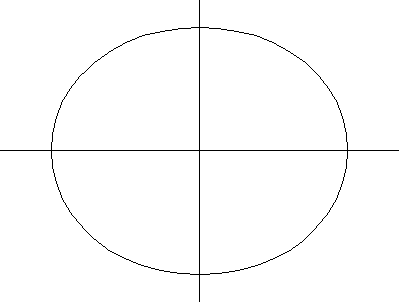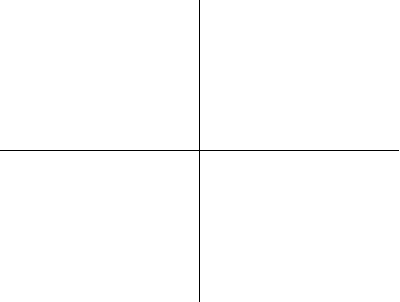
The above plots show a series of spiric sections for the ring torus, horn torus, and spindle
torus, respectively. When , the curve consists of two circles
of radius
whose centers are at
and
. If
, the curve consists of one point (the origin), while if
, no point lies on the curve.
The spiric extensions are an extension of the conic sections constructed by Menaechmus around 150 BC by cutting a cone by a plane, and were first considered around 50 AD by the Greek mathematician Perseus (MacTutor).
If ,
then (3) simplifies to
|
(4)
|
which is the equation of Cassini ovals. Cassini ovals are therefore spiric sections. Furthermore, the surface having these curves as cross sections is the Cassini surface illustrated above, with the modification that the vertical component is squared instead of to the fourth power.