A toric section is a curve obtained by slicing a torus (generally a horn torus) with a plane.
A spiric section is a special case of a toric section
in which the slicing plane is perpendicular to both the midplane of the torus and
to the plane .
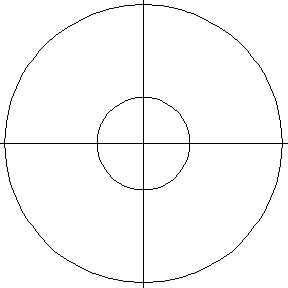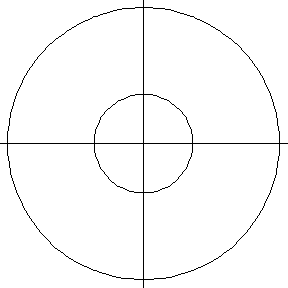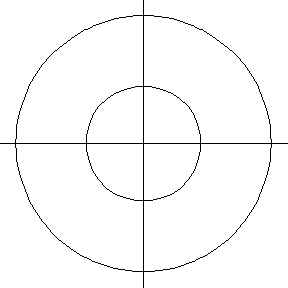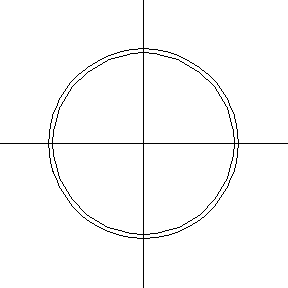
Consider a torus with tube radius . For a cutting plane parallel to the
-plane, the toric section is either a single circle (for
) or two concentric circles (for
). For planes containing
the z-axis, the section is two equal circles.
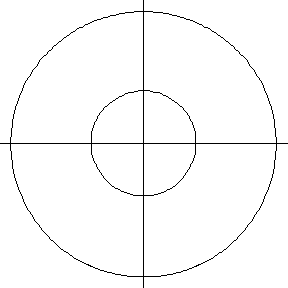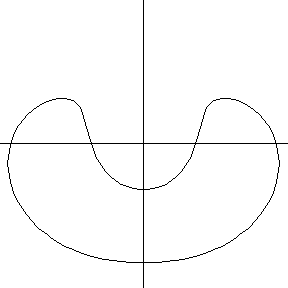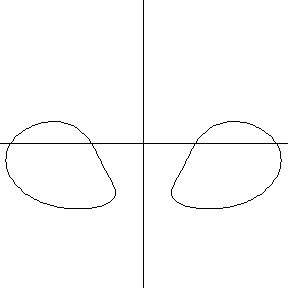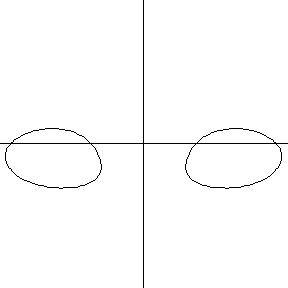
Toric sections at oblique angles can be more complicated, passing from a crescent shape, through a U-shape, and into two disconnected kidney-shaped curves.
Certain toric sections with cutting plane tangent to the torus along the circumference of its central hole, as illustrated above, resemble (but are not equivalent to) a
lemniscate curve. However, in the special case of
a torus with parameters ,
the toric section when the cutting plane is tangent to the torus along the circumference
of its central hole becomes exactly a lemniscate with
half-width