Quadrilateral

A quadrilateral, sometimes also known as a tetragon or quadrangle (Johnson 1929, p. 61) is a four-sided polygon. If not explicitly stated, all four polygon vertices are generally taken to lie in a plane. (If the points do not lie in a plane, the quadrilateral is called a skew quadrilateral.) There are three topological types of quadrilaterals (Wenninger 1983, p. 50): convex quadrilaterals (left figure), concave quadrilaterals (middle figure), and crossed quadrilaterals (or butterflies, or bow-ties; right figure).

A quadrilateral with two sides parallel is called a trapezoid, whereas a quadrilateral with opposite pairs of sides parallel is called a parallelogram.

For a planar convex quadrilateral (left figure above), let the lengths of the sides be , , , and , the semiperimeter , and the polygon diagonals and . The polygon diagonals are perpendicular iff .

An equation for the sum of the squares of side lengths is

(1)

where is the length of the line joining the midpoints of the polygon diagonals (Casey 1888, p. 22).

For bicentric quadrilaterals, the circumcircle and incircle satisfy

(2)

where is the circumradius, in the inradius, and is the separation of centers.

Given any five points in the plane in general position, four will form a convex quadrilateral. This result is a special case of the so-called happy end problem (Hoffman 1998, pp. 74-78).

There is a beautiful formula for the area of a planar convex quadrilateral in terms of the vectors corresponding to its two diagonals. Represent the sides of the quadrilateral by the vectors , , , and arranged such that and the diagonals by the vectors and arranged so that and . Then

			(3)
			(4)

where is the determinant and is a two-dimensional cross product.

There are a number of beautiful formulas for the area of a planar convex quadrilateral in terms of the side and diagonal lengths, including

			(5)
			(6)

(Beyer 1987, p. 123), Bretschneider's formula

			(7)
			(8)

(Coolidge 1939; Ivanoff 1960; Beyer 1987, p. 123) where is the semiperimeter, and the beautiful formula

(9)

(Bretschneider 1842; Strehlke 1842; Coolidge 1939; Beyer 1987, p. 123).

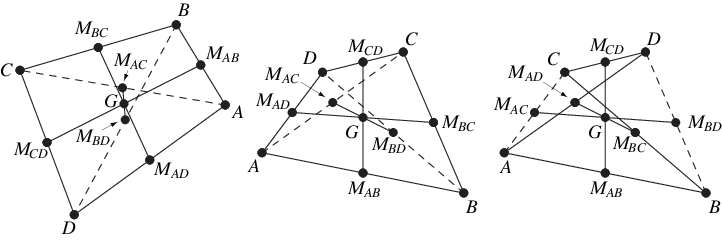
The centroid of the vertices of a quadrilateral occurs at the point of intersection of the bimedians (i.e., the lines and joining pairs of opposite midpoints) (Honsberger 1995, pp. 36-37). In addition, it is the midpoint of the line connecting the midpoints of the diagonals and (Honsberger 1995, pp. 39-40).

The four angle bisectors of a quadrilateral intersect adjacent bisectors in four concyclic points (Honsberger 1995, p. 35).

Any non-self-intersecting quadrilateral tiles the plane.

There is a relationship between the six distances , , , , , and between the four points of a quadrilateral (Weinberg 1972):

(10)

This can be most simply derived by setting the left side of the Cayley-Menger determinant

(11)

equal to 0 (corresponding to a tetrahedron of volume 0), thus giving a relationship between the distances between vertices of a planar quadrilateral (Uspensky 1948, p. 256).

A special type of quadrilateral is the cyclic quadrilateral, for which a circle can be circumscribed so that it touches each polygon vertex. Another special type is a tangential quadrilateral, for which a circle and be inscribed so it is tangent to each edge. A quadrilateral that is both cyclic and tangential is called a bicentric quadrilateral.

Wolfram Web Resources