A point lattice is a regularly spaced array of points.
In the plane, point lattices can be constructed having unit cells in the shape of a square, rectangle, hexagon, etc. Unless otherwise specified, point lattices
may be taken to refer to points in a square array, i.e., points with coordinates
, where
,
,
... are integers. Such an array is often called a grid or a mesh.
Point lattices are frequently simply called "lattices," which unfortunately conflicts with the same term applied to ordered sets treated in lattice theory. Every "point lattice" is a lattice under the ordering inherited from the plane, although a point lattice may not be a sublattice of the plane, since the infimum operation in the plane need not agree with the infimum operation in the point lattice. On the other hand, many lattices are not point lattices.
Properties of lattice are implemented in the Wolfram Language as LatticeData[lattice, prop].
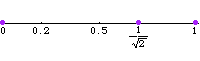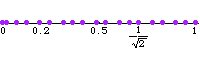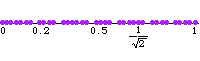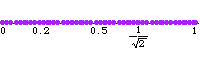
Formally, a lattice is a discrete subgroup of Euclidean space, assuming it contains the origin.
That is, a lattice is closed under addition and inverses, and every point has a neighborhood
in which it is the only lattice point. The common examples are and
. Usually, a lattice is defined to have full rank,
i.e., a lattice in
is the subgroup
|
(1)
|
where the
are integers and
are linearly independent vectors. Note that
a lattice needs at most
elements to generate it. For example, the subgroup
requires two generators but is not
discrete, and is not a lattice. The above illustration
shows that the subgroup generated by 1 and
is not a lattice by showing
for successive
.
The fraction of lattice points visible from the origin, as derived in Castellanos (1988, pp. 155-156), is
 |
(2)
| ||
 |
(3)
| ||
|
(4)
|
Therefore, this is also the probability that two randomly picked integers will be relatively prime to one another.
For ,
it is possible to select
lattice points with
such that no three are in a straight line. The number of
distinct solutions (not counting reflections and rotations) for
, 3, ..., are 1, 1, 4, 5, 11, 22, 57, 51, 156 ... (OEIS A000769). For large
, it is conjectured that it is only possible to select at most
lattice points with no three
collinear, where
|
(5)
|
(Guy and Kelly 1968; Guy 1994, p. 242). The number of the lattice points
which can be picked with no four concyclic
is
(Guy 1994, p. 241).
Any parallelogram on the lattice in which two opposite sides each have length 1 has unit area (Hilbert and Cohn-Vossen 1999, pp. 33-34).
A special set of polygons defined on the regular lattice are the golygons. A necessary and sufficient condition that a linear transformation transforms a lattice to itself is that it be unimodular. M. Ajtai has shown that there is no efficient algorithm for finding any fraction of a set of spanning vectors in a lattice having the shortest lengths unless there is an efficient algorithm for all of them (of which none is known). This result has potential applications to cryptography and authentication (Cipra 1996).