The homotopy groups generalize the fundamental group to maps from higher dimensional spheres, instead of from the circle. The th homotopy group of a topological
space
is the set of homotopy classes of maps from the
n-sphere to
, with a group structure, and is
denoted
.
The fundamental group is
, and, as in the case of
, the maps
must pass through a basepoint
. For
, the homotopy group
is an Abelian group.
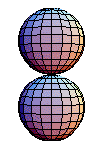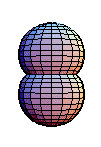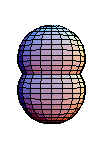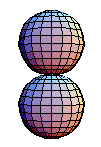
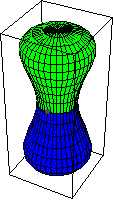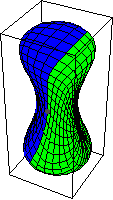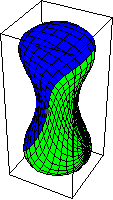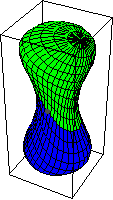
The group operations are not as simple as those for the fundamental group. Consider two maps and
, which pass through
. The product
is given by mapping the equator to the basepoint
. Then the northern hemisphere is mapped
to the sphere by collapsing the equator to a point, and then it is mapped to
by
. The southern hemisphere is similarly mapped to
by
. The diagram above shows the product of two spheres.

The identity element is represented by the constant map . The choice of direction of a loop in the fundamental
group corresponds to a manifold orientation
of
in a homotopy group. Hence the inverse of a map
is given by switching orientation for the sphere. By describing
the sphere in
coordinates, switching the first and second coordinate changes the orientation of
the sphere. Or as a hypersurface,
, switching orientation reverses the roles
of inside and outside. The above diagram shows that
is homotopic to the constant map, i.e., the identity. It
begins by expanding the equator in
, and then the resulting map is contracted to the basepoint.
As with the fundamental group, the homotopy groups do not depend on the choice of basepoint. But
the higher homotopy groups are always Abelian. The
above diagram shows an example of . The basepoint is fixed,
and because
the map can be rotated. When
, i.e., the fundamental
group, it is impossible to rotate the map while keeping the basepoint
fixed.
A space with
for all
is called
-connected.
If
is
-connected,
, then the Hurewicz homomorphism
from the
th-homotopy group to the
th-homology group is an isomorphism.
When
is a continuous map, then
is defined by taking the images under
of the spheres in
. The pushforward is natural, i.e.,
whenever the composition of two
maps is defined. In fact, given a fibration,
where
is pathwise-connected, there is a long
exact sequence of homotopy groups
 |