The great icosahedron, not to be confused with the great icosidodecahedron or great icosicosidodecahedron,
is the Kepler-Poinsot polyhedron whose
dual is the great
stellated dodecahedron. It is also the uniform
polyhedron with Maeder index 53 (Maeder 1997), Wenninger index 41 (Wenninger
1989), Coxeter index 69 (Coxeter et al. 1954), and Har'El index 58 (Har'El
1993). It has Schläfli symbol and Wythoff symbol
.
The great icosahedron can be constructed from an icosahedron with unit edge lengths by taking the 20 sets of vertices that are mutually spaced
by a distance ,
the golden ratio. The solid therefore consists of
20 equilateral triangles. The symmetry of their arrangement is such that the resulting
solid contains 12 pentagrams.
|
|
| |
|
|
|
|
The great icosahedron can most easily be constructed by building a "squashed" dodecahedron (top right figure) from the corresponding net (top left). Then, using the net shown in the bottom left figure, build 12 pentagrammic pyramids (bottom middle figure) and affix them into the dimples (bottom right). This method of construction is given in Cundy and Rollett (1989, pp. 98-99). If the edge lengths of the dodecahedron are unity, then the height of the pentagrammic pyramid (above the dodecahedron faces) is given by solving the equation for the edge length of a pentagonal pyramid
|
(1)
|
with ,
giving
|
(2)
|
The distance from the center of the dodecahedron to the apex of a pyramid is then given by
|
(3)
|
where
is the inradius of the dodecahedron.
The skeleton of the great icosahedron is isomorphic to the icosahedral graph.

The illustration above shows a paper sculpture of the great icosahedron. Each facial plane of the model is a different color, but with pairs of parallel faces given the same color. The model is made from 180 pieces.
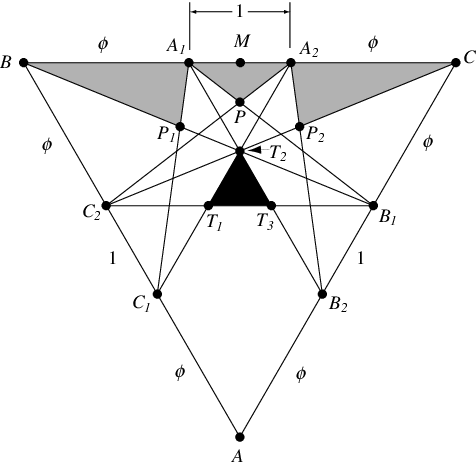
The dimensions of the pentagrammic pyramid can be by examining a triangular section of the great icosahedron. In this triangle, each side is divided in the ratios , and lines are drawn as shown.
Then the light shaded portions on the left and right correspond to sides of two pyramids
and the center shaded portion is the "lip" of the pyramid between the first
two pyramids. Furthermore, the filled portion of the diagram corresponds to one face
of the icosahedron inscribed in the great icosahedron.
In the notation of the figure above,
|
(4)
| |||
|
(5)
| |||
|
(6)
| |||
|
(7)
| |||
|
(8)
|
The great icosahedron constructed from the dodecahedron with unit edge lengths has edge lengths (where edges are interpreted to be broken where facial plane intersect) given by
|
(9)
| |||
|
(10)
| |||
|
(11)
| |||
|
(12)
|
Its circumradius is
|
(13)
|
and the surface area and volume are then
|
(14)
| |||
|
(15)
| |||
|
(16)
|
The convex hull of the great icosahedron is a regular icosahedron and the dual of the icosahedron is the dodecahedron, so the dual of the great icosahedron is one of the dodecahedron stellations (Wenninger 1983, p. 40)