 |
A complex number 
may be represented as
 |
(1)
|
where 
is a positive real number called the complex modulus
of 
,
and 
(sometimes also denoted 
) is a real number called the argument. The argument is sometimes
also known as the phase or, more rarely and more confusingly,
the amplitude (Derbyshire 2004, pp. 180-181 and 376).
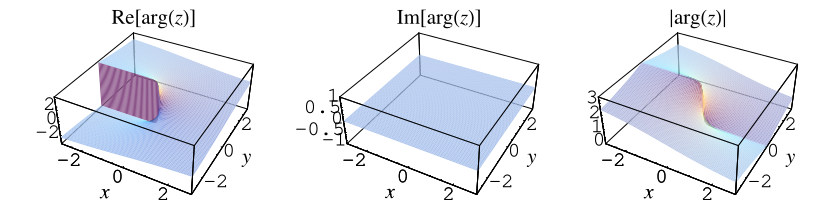
The complex argument of a number 
is implemented in the Wolfram
Language as Arg[z].
The complex argument can be computed as
 |
(2)
|
Here, 
,
sometimes also denoted 
,
corresponds to the counterclockwise angle from the positive real axis, i.e., the value of 
such that 
and 
. The special kind of inverse
tangent used here takes into account the quadrant in which 
lies and is returned by the FORTRAN command ATAN2(y,
x) and the Wolfram Language function
ArcTan[x,
y], and is often (including by the Wolfram
Language function Arg)
restricted to the range 
. In the degenerate case when 
,
 |
(3)
|
Special values of the complex argument include
 |  |  |
(4)
|
 |  |  |
(5)
|
 |  |  |
(6)
|
 |  |  |
(7)
|
 |  |  |
(8)
|
From the definition of the argument, the complex argument of a product of two numbers is equal to the sum of their arguments,
 |  |  |
(9)
|
 |  |  |
(10)
|
 |  | ![arg[e^(i(theta_z+theta_w))]](/images/equations/ComplexArgument/Inline38.svg) |
(11)
|
 |  |  |
(12)
|
It therefore follows that
 |
(13)
|
giving the special case
 |
(14)
|
Note that all these identities will hold only modulo factors of 
if the argument is being restricted to ![theta in (-pi,pi]](/images/equations/ComplexArgument/Inline43.svg)
.
