Inverse Tangent

The inverse tangent is the multivalued function (Zwillinger 1995, p. 465), also denoted (Abramowitz and Stegun 1972, p. 79; Harris and Stocker 1998, p. 311; Jeffrey 2000, p. 124) or (Spanier and Oldham 1987, p. 333; Gradshteyn and Ryzhik 2000, p. 208; Jeffrey 2000, p. 127), that is the inverse function of the tangent. The variants (e.g., Bronshtein and Semendyayev, 1997, p. 70) and are sometimes used to refer to explicit principal values of the inverse tangent, although this distinction is not always made (e.g., Zwillinger 1995, p. 466).

The inverse tangent function is plotted above along the real axis.

Worse yet, the notation is sometimes used for the principal value, with being used for the multivalued function (Abramowitz and Stegun 1972, p. 80). Note that in the notation (commonly used in North America and in pocket calculators worldwide), denotes the tangent and the inverse function, not the multiplicative inverse.

The principal value of the inverse tangent is implemented as ArcTan[z] in the Wolfram Language. In the GNU C library, it is implemented as atan(double x).

The inverse tangent is a multivalued function and hence requires a branch cut in the complex plane, which the Wolfram Language's convention places at and . This follows from the definition of as

In the Wolfram Language (and in this work), this branch cut definition determines the range of for a real number as . Other continuous real branches differ by integer multiples of (NIST 2026, eq. 4.23.33).

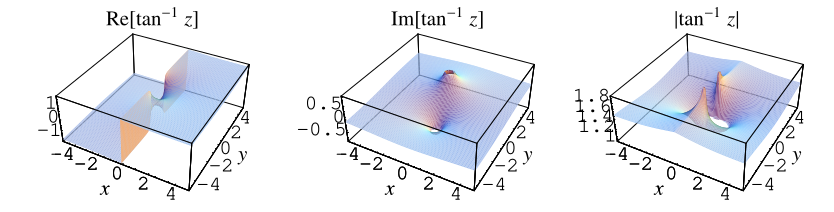
The inverse tangent function is plotted above in the complex plane.

has the special values

The derivative of is

and the indefinite integral is

For a real number , the derivative is times the probability density function of the standard Cauchy distribution.

For a complex number with real numbers and , its complex argument is

where , sometimes also denoted , corresponds to the counterclockwise angle from the positive real axis, i.e., the value of such that and , where . Plots of are illustrated above for real number values of and .

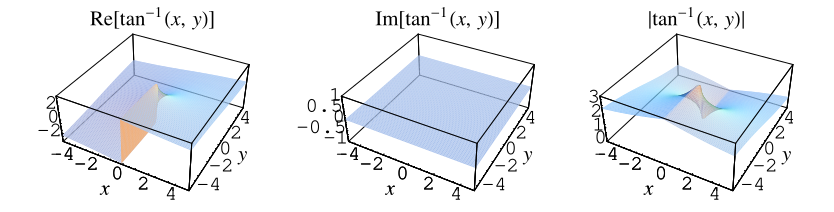
The two-argument inverse tangent takes into account the quadrant in which lies. It is returned by the FORTRAN command ATAN2(y, x), the GNU C library command atan2(double y, double x), and the Wolfram Language command ArcTan[x, y], with the range . In the degenerate case when ,

For , the usual has the Maclaurin series

(OEIS A033999 and A005408). The series also converges at the real endpoints . A more rapidly converging form due to Euler is given by

for a real number (Castellanos 1988). This is related to the formula of Euler given by

where

and , with the value at 0 obtained by a limit.

Abrarov and Quine (2018) give the series

for a real number . Each of the two complex component series is absolutely convergent, with limiting ratio of successive term absolute values , compared with for Euler's series.

The inverse tangent formulas are connected with many interesting approximations to pi. For ,

(OEIS A075553 and A075554).

The inverse tangent satisfies

for ,

for all complex number arguments ,

for all real number arguments , where equality for the last equation is understood to be in the limit as , and

In terms of the hypergeometric function,

for complex number arguments , and

for a real number (Castellanos 1988).

Castellanos (1986, 1988) also gives some curious formulas in terms of the Fibonacci numbers,

where , , and is the largest positive root of

The first series is valid for a real number with . The second and third series are valid for .

For a real number and a positive integer , Abrarov et al. (2021) give the finite sum

For a short proof, the difference equals the th summand. Both sides lie between and , and applying the tangent addition formula gives equality. The sum therefore telescopes.

The inverse tangent satisfies the addition formula

for , as well as the more complicated formula

valid for a real number . For general complex number arguments, a multiple of may be required to account for the branches. An additional identity known to Euler is given by

for or . Another interesting inverse tangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938; Castellanos 1988; Bromwich 1991) is

where

and .

The inverse tangent has continued fraction representations

(Lambert 1770; Lagrange 1776; Wall 1948, p. 343; Olds 1963, p. 138) and

due to Euler and sometimes known as Euler's continued fraction (Borwein et al. 2004, p. 30).

To find numerically for a real number , the following arithmetic-geometric mean-like algorithm can be used. Let

Then compute

and the inverse tangent is given by

(Acton 1990).

An inverse tangent with a positive integer is called reducible if it is expressible as a finite sum of the form

where are positive or negative integers and are positive integers . is reducible iff all the prime factors of occur among the prime factors of for , ..., . A second necessary and sufficient condition is that the largest prime factor of is less than . Equivalent to the second condition is the statement that every Gregory number can be uniquely expressed as a sum in terms of s for which is a Størmer number (Conway and Guy 1996). To find this decomposition, write

so the ratio

is a rational number. Equation (50) can also be written

Writing (48) in the form

allows a direct conversion to a corresponding inverse cotangent formula

where

Todd (1949) gives a table of decompositions of for . Conway and Guy (1996) give a similar table in terms of Størmer numbers.

Arndt and Gosper give the inverse tangent identity (Gosper 1997), valid for real numbers and a nonnegative integer ,

There is an amazing set of BBP-type formulas for :

One of these formulas is requested as a problem by Bailey et al. (2007, p. 225).

Casper (2026) reported that the principal real inverse tangent of every nonzero rational number has irrationality measure 2, extending an OpenAI interpolation and determinant argument with Gaussian integers. The work credits AI assistance with proof development and Lean formalization. As of Oct. 25, 2026, independent specialist review had not been reported.