A cellular automaton is a collection of "colored" cells on a grid of specified shape that evolves through a number of discrete time steps according to a set of rules based on the states of neighboring cells. The rules are then applied iteratively for as many time steps as desired. von Neumann was one of the first people to consider such a model, and incorporated a cellular model into his "universal constructor." Cellular automata were studied in the early 1950s as a possible model for biological systems (Wolfram 2002, p. 48). Comprehensive studies of cellular automata have been performed by S. Wolfram starting in the 1980s, and Wolfram's fundamental research in the field culminated in the publication of his book A New Kind of Science (Wolfram 2002) in which Wolfram presents a gigantic collection of results concerning automata, among which are a number of groundbreaking new discoveries.
The Season 2 episode "Bettor or Worse" (2006) of the television crime drama NUMB3RS mentions one-dimensional cellular automata.
Cellular automata come in a variety of shapes and varieties. One of the most fundamental properties of a cellular automaton is the type of grid on
which it is computed. The simplest such "grid" is a one-dimensional line.
In two dimensions, square, triangular,
and hexagonal grids may be considered. Cellular
automata may also be constructed on Cartesian grids in arbitrary numbers of dimensions,
with the -dimensional
integer lattice
being the most common choice. Cellular automata on a
-dimensional integer lattice are implemented in the Wolfram
Language as CellularAutomaton[rule,
init, steps].
The number of colors (or distinct states) a cellular automaton may assume must also be specified. This
number is typically an integer, with
(binary) being the simplest choice. For a binary automaton,
color 0 is commonly called "white," and color 1 is commonly called "black".
However, cellular automata having a continuous range of possible values may also
be considered.
In addition to the grid on which a cellular automaton lives and the colors its cells may assume, the neighborhood over which cells affect one another must also be specified. The simplest choice is "nearest neighbors," in which only cells directly adjacent to a given cell may be affected at each time step. Two common neighborhoods in the case of a two-dimensional cellular automaton on a square grid are the so-called Moore neighborhood (a square neighborhood) and the von Neumann neighborhood (a diamond-shaped neighborhood).
The simplest type of cellular automaton is a binary, nearest-neighbor, one-dimensional automaton. Such automata were called "elementary cellular automata" by S. Wolfram, who has extensively studied their amazing properties (Wolfram 1983; 2002, p. 57). There are 256 such automata, each of which can be indexed by a unique binary number whose decimal representation is known as the "rule" for the particular automaton. An illustration of rule 30 is shown above together with the evolution it produces after 15 steps starting from a single black cell.
A slightly more complicated class of cellular automata are the nearest-neighbor, -color,
one-dimensional totalistic cellular automata.
In such automata, it is the average of adjacent cells that determine the evolution,
and the simplest nontrivial examples have
colors. For these automata, the set of rules describing
the behavior can be encoded as a
-digit
-ary number known as a "code." The rules and 300
steps of the ternary (
) code 912 automaton are illustrated
above.
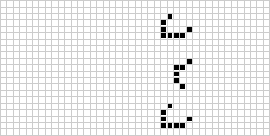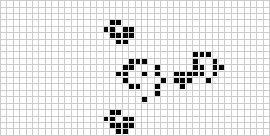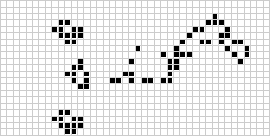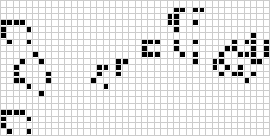
In two dimensions, the best-known cellular automaton is Conway's game of life, discovered by J. H. Conway in 1970 and popularized in Martin
Gardner's Scientific American columns. The game
of life is a binary () totalistic
cellular automaton with a Moore neighborhood
of range
.
Although the computation of successive game of life
generations was originally done by hand, the computer revolution soon arrived and
allowed more extensive patterns to be studied and propagated. An animation of the
game of life construction known as a puffer train
is illustrated above.
WireWorld is another common two-dimensional cellular automaton.
The theory of cellular automata is immensely rich, with simple rules and structures being capable of producing a great variety of unexpected behaviors. For example, there exist universal cellular automata that are capable of simulating the behavior of any other cellular automaton or Turing machine. It has even been proved by Gacs (2001) that there exist fault-tolerant universal cellular automata, whose ability to simulate other cellular automata is not hindered by random perturbations provided that such perturbations are sufficiently sparse.