Rule 90 is one of the elementary cellular automaton rules introduced by Stephen Wolfram in 1983 (Wolfram 1983, 2002). It
specifies the next color in a cell, depending on its color and its immediate neighbors.
Its rule outcomes are encoded in the binary representation
. This rule is illustrated
above together with the evolution of a single black cell it produces after 15 steps
(Wolfram 2002, p. 55).
Starting with a single black cell, successive generations are given by interpreting the numbers 1, 5, 17, 85, 257, 1285, 4369, 21845, ... (OEIS A038183) in binary, namely as 1, 101, 10001, 1010101, 100000001, ... (OEIS A070886).
Rule 90 is amphichiral, and its complement is rule 165.
The fractal produced by this rule was described by Sierpiński in 1915 and appearing in Italian art from the 13th century (Wolfram 2002, p. 43).
It is therefore also known as the Sierpiński
sieve, Sierpiński gasket, or Sierpiński triangle. The binomial
coefficient
mod 2 can be computed using the XOR operation
XOR
,
making Pascal's triangle mod 2 very easy to construct.
Moreover, coloring all odd numbers black and even
numbers white in Pascal's triangle produces a
Sierpiński sieve (Guy 1990; Wolfram 2002,
p. 870).
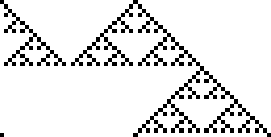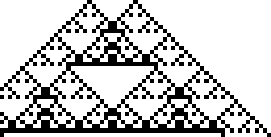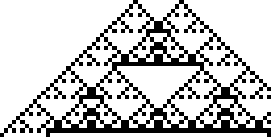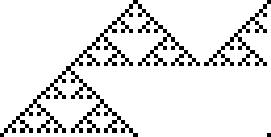
Rule 90 is one of the eight additive elementary cellular automata (Wolfram 2002, p. 952).