The game of life is the best-known two-dimensional cellular automaton, invented by John H. Conway and popularized in Martin Gardner's Scientific American column starting in October 1970. The game of life was originally played (i.e., successive generations were produced) by hand with counters, but implementation on a computer greatly increased the ease of exploring patterns.
The life cellular automaton is run by placing a number of filled cells on a two-dimensional grid. Each generation then switches cells on or off depending on the state of the cells that surround it. The rules are defined as follows. All eight of the cells surrounding the current one are checked to see if they are on or not. Any cells that are on are counted, and this count is then used to determine what will happen to the current cell.
1. Death: if the count is less than 2 or greater than 3, the current cell is switched off.
2. Survival: if (a) the count is exactly 2, or (b) the count is exactly 3 and the current cell is on, the current cell is left unchanged.
3. Birth: if the current cell is off and the count is exactly 3, the current cell is switched on.
The game of life is a totalistic cellular automaton, and can be implemented as follows using the built-in command CellularAutomaton,
where the initial conditions are specified
as a binary matrix
and the results for generations
through
are returned. (Here,
corresponds to the initial pattern.)
Life[m_List?MatrixQ, {g1_Integer, g2_Integer}] :=
CellularAutomaton[
{
224,
{2, {{2, 2, 2}, {2, 1, 2}, {2, 2, 2}}},
{1, 1}
},
{m, 0},
g2,
{
{g1, g2},
Automatic
}] /; g2>=g1
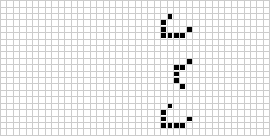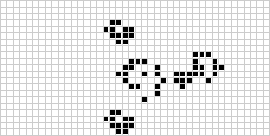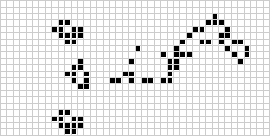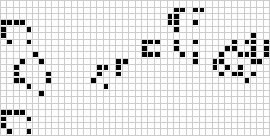
A pattern which does not change from one generation to the next is known as a still life, and is said to have period 1. Several still lifes are illustrated above. The
numbers of still lives of
cells for
,
2, 3, ... are 0, 0, 0, 2, 1, 5, 4, 9, 10, 25, 46, 121, 240, 619, 1353, ... (OEIS
A019473).
Patterns that cycle through a set of configurations are called oscillators.
Conway originally believed that no pattern could produce an infinite number of cells, and offered a $50 prize to anyone who could find a counterexample before the end of 1970 (Gardner 1983, p. 216). Many counterexamples were subsequently found, including guns and puffer trains (illustrated above).
A life pattern which has no father pattern is known as a Garden of Eden (for obvious biblical reasons). The first such pattern was not found until 1971 and many are now known (LifeWiki).

The long-open "unique father problem" of determining if a pattern exists which has a father pattern but no grandfather pattern (Wainwright 1972, Gardner 1983, p. 249), was settled by Ilkka Törmä and Ville Salo in January 2022 with the discovery of a 374-cell example of such a pattern, a result that was quickly reduced to the 306-cell pattern illustrated above (apgoucher 2022, LifeWiki).
Amazingly, life is a universal cellular automaton, in the sense that it is effectively capable of emulating any cellular
automaton, Turing machine, or any other system
that can be translated into a system known to be universal.
The outlines of a proof for life's universality
were given by Berlekamp et al. (1982) and independently by Gosper (Gardner
1983, pp. 250-253). Around 2000, a Turing machine
that can be extended to a universal Turing
machine was explicitly implemented in life by P. Rendell (Rendell, Adamatzky
2001). While Rendell's machine can be made into a "true" universal computer
simply by making his tape infinite, he neither noted this fact nor provided an actual
construction of a universal Turing machine.
Subsequently, on November 11, 2002, P. Chapman constructed a life pattern based
on D. Hickerson's "sliding block memory" approach that implements
the actions of a universal register
machine. Unlike the finite tape of Rendell's Turing
machine, the values in the registers of Chapman's machine are unbounded, making
it a true model of universal computation in the game of life. Chapman's construction
uses live cells in an area of
, and can calculate approximately 20 generations
per second on a 400 MHz computer.
More amazingly still, as shown by Wolfram (2002), even one-dimensional cellular automata (in particular, rule 110), can be universal.
Two-dimensional cellular automaton games similar to life but with different rules have been constructed and given the names HexLife and HighLife. HashLife is a life algorithm that achieves remarkable speed by storing subpatterns in a hash table and using them to skip forward, sometimes thousands of generations at a time.