Echidnahedron

The "echidnahedron" is the term apparently first used in the Netlib polyhedron database for the "complete" icosahedron stellation (Coxeter et al. 1999, pp. 13, 30-32, and 64). The echidnahedron has original Maeder index 4 (Maeder 1994), Maeder circumradius index 59, Coxeter number 8, Coxeter §2 notation 13, Coxeter §3 notation H, Wenninger number 42 (Wenninger 1971, p. 65), Wheeler number 12 (Wheeler 1924), appears in Coxeter et al. (1999, p. 31) as Plate III, and in Brückner (1900) as Fig. 14, Taf. XI.

It is implemented in the Wolfram Language as PolyhedronData["Echidnahedron"].

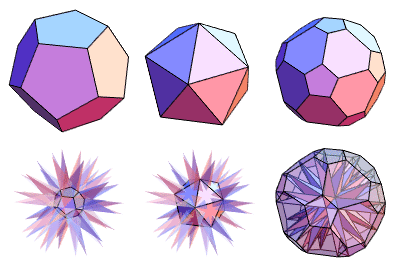
It has 92 vertices, 270 edges, and 180 faces. Its vertices are arranged in three concentric groups of 20 (indicated in red in the above illustration), 12 (green), and 60 (blue).

For an echidnahedron with edge lengths , , , and (where is the golden ratio), the vertices determine a regular dodecahedron, regular icosahedron, and (irregular) truncated icosahedron, with circumradii

			(1)
			(2)
			(3)

respectively.

The surface area and volume are given by

			(4)
			(5)

A solid echidnahedron has moment of inertia tensor

(6)

for uniform density solid of mass .