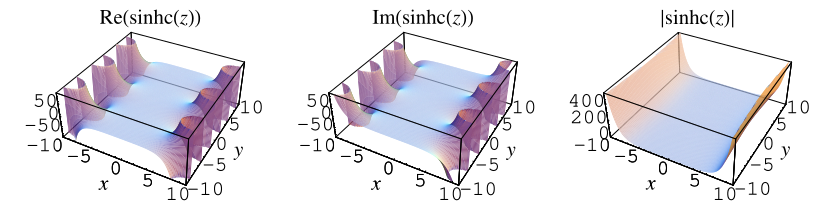
By analogy with the sinc function, define the sinhc function by
 |
(1)
|
Since
is not a cardinal function, the "analogy"
with the sinc function is one of functional structure,
not mathematical properties. It is quite possible that a better term than
could be coined, although there appears to be no other
name previously assigned to this function.
The function has derivative
|
(2)
|
|
(3)
|
where
is the Shi function.
The function has real fixed points at 1.31328371835... (OEIS A133916) and 2.63924951389... (OEIS A133917).