TOPICS
Search

Rogers-Ramanujan Continued Fraction

DOWNLOAD Mathematica NotebookDownload Wolfram Notebook
RogersRamanujanR

The Rogers-Ramanujan continued fraction is a generalized continued fraction defined by

R(q)=(q^(1/5))/(1+q/(1+(q^2)/(1+(q^3)/(1+...))))
(1)

(Rogers 1894, Ramanujan 1957, Berndt et al. 1996, 1999, 2000). It was discovered by Rogers (1894), independently by Ramanujan around 1913, and again independently by Schur in 1917. Modulo the factor of q^(1/5) added for convenience, it provides a geometric series q-analog of the golden ratio

phi=1+1/(1+1/(1+1/(1+...))).
(2)

The convergents A_n(q)/B_n(q) of q^(-1/5)R(q) are given by

A_0(q)=1
(3)
A_1(q)=1
(4)
A_n(q)=A_(n-1)(q)+q^nA_(n-2)(q)
(5)
B_(-1)(q)=1
(6)
B_0(q)=1
(7)
B_n(q)=B_(n-1)(q)+q^nB_(n-2)(q)
(8)

(OEIS A128915 and A127836; Sills 2003, p. 25, identity 3-14).

The fraction can be expressed in closed form in terms of q-series by

R(q)=q^(1/5)((q;q^5)_infty(q^4;q^5)_infty)/((q^2;q^5)_infty(q^3;q^5)_infty)
(9)
=q^(1/5)product_(k=0)^(infty)((1-q^(5k+1))(1-q^(5k+4)))/((1-q^(5k+2))(1-q^(5k+3)))
(10)
=q^(1/5)product_(k=1)^(infty)((1-q^(5k-1))(1-q^(5k-4)))/((1-q^(5k-2))(1-q^(5k-3))),
(11)

and in terms of the Ramanujan theta function

f(a,b)=sum_(n=-infty)^inftya^(n(n+1)/2)b^(n(n-1)/2)
(12)

by

R(q)=q^(1/5)(f(-q,-q^4))/(f(-q^2,-q^3)).
(13)

In the upper half-plane and modulo branch cuts, it can also be expressed exactly in terms of the Dedekind eta function eta(tau) by

R(q)=1/2(sqrt(x^2+2x+5)-x-1),
(14)

where

x=(eta(-(ilnq)/(10pi)))/(eta(-(iln(q^5))/(2pi)))
(15)

(Trott 2004).

The coefficients of q^n in the Maclaurin series of R(q)/q^(1/5) for n=0, 1, 2, ... are 1, -1, 1, 0, -1, 1, -1, 1, 0, -1, 2, -3, ... (OEIS A007325).

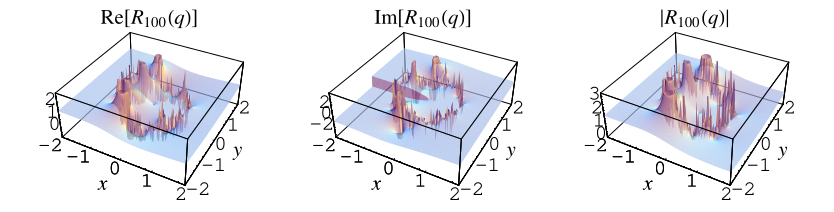
RogersRamanujanRReIm100
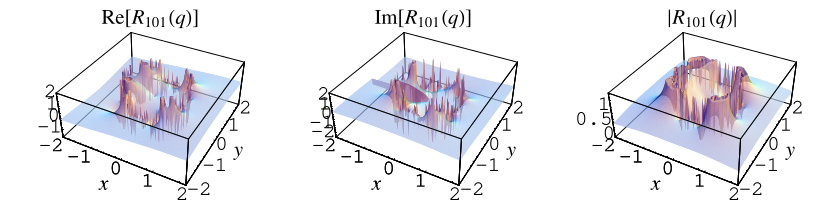
RogersRamanujanRReIm101
RogersRamanujanRContours100
RogersRamanujanRContours101

The fraction converges quickly for points sufficiently far from the unit circle in the complex plane. For values |q|<1, the series converges to a unique value, while for |q|>1, it converges to two possible values. The value of the nth convergent of the continued fraction R_n(q) can be expressed in terms of the unique value inside the unit disk as

R_n(q)={q^(1/5)(-q^(-1))^(-1/5)[R_n(-q^(-1))]^(-1) for n even; q^(-4/5)(q^(-4))^(-1/5)R(q^(-4)) for n odd
(16)

(Andrews et al. 1992, Trott 2004).

Amazingly, Ramanujan showed that R(e^(-pisqrt(n))) is an algebraic number for all positive rational r. Special cases include

R(1)=phi-1
(17)
R(e^(-pi))=r_1
(18)
R(e^(-2pi))=-phi+sqrt(1/2(5+sqrt(5))),
(19)

where r_1 is the root of x^8+14x^7+22x^6+22x^5+30x^4-22x^3+22x^2-14x+1 near 0.51142.... r_1 can be written as

r_1=1/8(3+sqrt(5))(RadicalBox[5, 4]-1)(sqrt(10+2sqrt(5))-(3+RadicalBox[5, 4])(RadicalBox[5, 4]-1))
(20)

(Yi 2001, Trott 2004). The values of r_n have been computed by Trott for all values of n>=10, and the algebraic degrees of r_1, r_2, ... are 8, 4, 32, 8, 40, 16, 64, 16, 96, 20, ... (OEIS A082682; Trott 2004).

R(q) satisfies the amazing equalities

1/(R(q))-1-R(q)=((q^(1/5))_infty)/(q^(1/5)(q^5)_infty)
(21)
1/([R(q)]^5)-11-[R(q)]^5=((q)_infty^6)/(q(q^5)_infty^6),
(22)

where (q)_infty=(q;q)_infty is a q-Pochhammer symbol. It also satisfies

sum_(n=-infty)^(infty)(-1)^n(10n+3)q^((5n+3)n/2)=[3/([R(q)]^2)+[R(q)]^3]q^(2/5)(q^5)_infty^3
(23)
sum_(n=-infty)^(infty)(-1)^n(10n+1)q^((5n+1)n/2)=[1/([R(q)]^3)-3[R(q)]^2]q^(3/5)(q^5)_infty^3
(24)

(Watson 1929ab; Berndt 1991, pp. 265-267; Berndt et al. 1996, 2000; Son 1998).

Defining

u=R(q)
(25)
u^'=-R(-q)
(26)
v=R(q^2)
(27)
w=R(q^4),
(28)

these quantities satisfy the modular equations

uv^2=(v-u^2)/(v+u^2)
(29)
uw=(w^2-u^2v)/(w+v^2)
(30)
vw^2=(w-v^2)/(w+v^2)
(31)
uu^'v^2=(uu^'-v)/(u^'-u)
(32)
u^'w=(u^('2)-w)/(v^2+w)
(33)
-vw=(u^'(v^2-w))/(u^('2)v-w)
(34)
uu^'v=(u^'-u)/(v+uu^')
(35)
vw=(u(v^2-w))/(u^2v-w)
(36)

(Berndt et al. 1996, 2000). Trott (2004) gives modular equations of orders 2 to 15 and the primes 17, 19, and 23.

As discussed by Hardy (Ramanujan 1962, pp. xxvii and xxviii), Berndt and Rankin (1995), and Berndt et al. (1996, 2000), Ramanujan also defined the generalized continued fraction

R(a,q)=1/(1+(aq)/(1+(aq^2)/(1+(aq^3)/(1+...)))).
(37)
RogersRamanujanF
RogersRamanujanFReIm
RogersRamanujanFContours

Ramanujan also considered the continued fraction

F(a,q)=1-(aq)/(1-(aq^2)/(1-(aq^3)/(1-...)))
(38)
=(sum_(k=0)^(infty)((-a)^kq^(k^2))/((q)_k))/(sum_(k=0)^(infty)((-a)^kq^(k(k+1)))/((q)_k)).
(39)

(Berndt 1991, p. 30; Berndt et al. 1996, 2000), of which the special case F(q)=F(1,q) is plotted above.

Terminating at a term aq^n gives

(sum_(k=0)^(|_(n+1)/2_|)((-a)^kq^(k^2)(q)_(n-k+1))/((q)_k(q)_(n-2k+1)))/(sum_(k=0)^(|_n/2_|)((-a)^kq^(k(k+1))(q)_(n-k))/((q)_k(q)_(n-2k)))=1-(aq)/(1-(aq^2)/(1-(aq^3)/(1-...-(aq^n)/1))),
(40)

(Berndt et al. 1996, 2000).

The real roots of F(q) are 0.576149, 0.815600, 0.882493, 0.913806, 0.931949, 0.943785, 0.952125, ..., the smallest of which was found by Ramanujan (Berndt et al. ). F(q) and its smallest positive root are related to the enumeration of coins in a fountain (Berndt 1991, Berndt et al. 1996, 2000) and the study of birth and death processes (Berndt et al. 1996, 2000; Parthasarathy et al. 1998). In general, the least positive root q_0(a) of F(a,q) is given as a->infty by

q_0(a)∼1/a-1/(a^2)+2/(a^3)-6/(a^4)+(21)/(a^5)-(79)/(a^6)+(311)/(a^7)-(1266)/(a^8) +(5289)/(a^9)-(22553)/(a^(10))+(97753)/(a^(11))-...
(41)

(OEIS A050203; Berndt et al. 1996, 2000). Ramanujan gave the amazing approximations

q_0^((1))(a)∼2/(a-1+sqrt((a+1)(a+5)))+O(a^(-8))
(42)
q_0^((2))(a)∼1/((a-1+sqrt((a+1)(a+5)))/2+[(a+3-sqrt((a+1)(a+5)))/(a-1+sqrt((a+1)(a+5)))]^3)+O(a^(-11)).
(43)

For a=1, these approximations give

q_0^((1))(1)=1/3sqrt(3) approx 0.57735
(44)
q_0^((2))(1)=3/(110)(9+7sqrt(3)) approx 0.576119.
(45)

More generally, for the broad class of q^_ defined as q^_=e^(2piitau), R(q) can be evaluated in terms of the j-function j(tau) and the icosahedral equation as

j(tau)=-((r^(20)-228r^(15)+494r^(10)+228r^5+1)^3)/(r^5(r^(10)+11r^5-1)^5)
(46)

with one of the r_i as r=R(q) (Duke 2004). As an example, R(e^(-2pi)) has tau=sqrt(-1)=i, so j(tau)=12^3. Substituting 12^3 into the equation, one of its factors will be a quartic with the root r=R(e^(-2pi)).

Furthermore, the numerator and the denominator (with a constant) can be combined to form a perfect square,

(r^(20)-228r^(15)+494r^(10)+228r^5+1)^3+1728r^5(r^(10)+11r^5-1)^5 =(r^(30)+522r^(25)-10005r^(20)-10005r^(10)-522r^5+1)^2,
(47)

which are in fact polynomial invariants of the icosahedral group.

See also

Bauer-Muir Transformation, Fountain, Generalized Continued Fraction, Golden Ratio, q-Series, Ramanujan Theta Functions, Rogers-Ramanujan Identities

Portions of this entry contributed by Tito Piezas III

Explore with Wolfram|Alpha

References

Andrews, G. On the General Rogers-Ramanujan Theorem. Providence, RI: Amer. Math. Soc., 1974.Andrews, G. E.; Berndt, B. C.; Jacobsen, L.; and Lamphere, R. L. The Continued Fractions Found in the Unorganized Portion of Ramanujan's Notebooks. Providence, RI: Amer. Math. Soc., 1992.Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W. "Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113, 481-509, 2006.Berndt, B. C. Ramanujan's Notebooks, Part III. New York: Springer-Verlag, 1991.Berndt, B. C. "Continued Fractions." Ch. 32 in Ramanujan's Notebooks, Part V. New York: Springer-Verlag, pp. 9-88, 1998.Berndt, B. C. and Chan, H. H. "Some Values for the Rogers-Ramanujan Continued Fraction." Canad. J. Math. 47, 897-914, 1995.Berndt, B. C. and Rankin, R. A. Ramanujan: Letters and Commentary. Providence, RI: Amer. Math. Soc, 1995.Berndt, B. C.; Chan, H. H.; and Zhang, L.-C. "Explicit Evaluations of the Rogers-Ramanujan Continued Fraction." J. reine angew. Math. 480, 141-159, 1996.Berndt, B. C.; Chan, H. H.; Huang, S.-S.; Kang, S.-Y.; Sohn, J.; and Son, S. H. "The Rogers-Ramanujan Continued Fraction." J. Comput. Appl. Math. 105, 9-24, 1999.Berndt, B. C.; Huang, S.-S.; Sohn, J.; and Son, S. H. "Some Theorems on the Rogers-Ramanujan Continued Fraction in Ramanujan's Lost Notebook." Trans. Amer. Math. Soc. 352, 2157-2177, 2000.Duke, W. "Continued Fractions and Modular Functions." Bull. Amer. Math. Soc. 42, 137-162, 2005.Joyce, G. S. "Exact Results for the Activity and Isothermal Compressibility of the Hard-Hexagon Model." J. Phys. A: Math. Gen. 21, L983-L988, 1988.Parthasarathy, P. R.; Lenin, R. B.; Schoutens, W.; and van Assche, W. "A Birth and Death Process Related to the Rogers-Ramanujan Continued Fraction." J. Math. Anal. Appl. 224, 297-315, 1998.Ramanathan, K. G. "On Ramanujan's Continued Fraction." Acta Arith. 43, 209-226, 1984a.Ramanathan, K. G. "On the Rogers-Ramanujan Continued Fraction." Proc. Indian Acad. Sci. (Math. Sci.) 93, 67-77, 1984b.Ramanathan, K. G. "Ramanujan's Continued Fraction." Indian J. Pure Appl. Math. 16, 695-724, 1985.Ramanathan, K. G. "Some Applications of Kronecker's Limit Formula." J. Indian Math. Soc. 52, 71-89, 1987.Ramanujan, S. Notebooks (2 Volumes). Bombay, India: Tata Institute, 1957.Ramanujan, S. Collected Papers. New York: Chelsea, 1962.Rogers, L. J. "Second Memoir on the Expansion of Certain Infinite Products." Proc. London Math. Soc. 25, 318-343, 1894.Rogers, L. J. "On a Type of Modular Equations." Proc. London Math. Soc. 19, 387-397, 1920.Sills, A. V. "Finite Rogers-Ramanujan Type Identities." Electron. J. Combin. 10, No. 13, 2003.Sloane, N. J. A. Sequences A007325/M0415, A050203, A082682, A127836, and A128915 in "The On-Line Encyclopedia of Integer Sequences."Son, S. H. "Some Theta Function Identities Related to the Rogers-Ramanujan Continued Fraction." Proc. Amer. Math. Soc. 126, 2895-2902, 1998.Trott, M. "Modular Equations of the Rogers-Ramanujan Continued Fraction." Mathematica J. 9,314-333, 2004.Watson, G. N. "Theorems Stated by Ramanujan (VII): Theorems on Continued Fractions." J. London Math. Soc. 4, 39-48, 1929a.Watson, G. N. "Theorems Stated by Ramanujan (IX): Two Continued Fractions." J. London Math. Soc. 4, 231-237, 1929b.Yi, J. "Evaluations of the Rogers-Ramanujan Continued Fraction R(q) by Modular Equations." Acta Arith. 97, 103-127, 2001.Yi, J. "Modular Equations for the Rogers-Ramanujan Continued Fraction and the Dedekind Eta-Function." Ramanujan J. 5, 377-384, 2002.

Referenced on Wolfram|Alpha

Rogers-Ramanujan Continued Fraction

Cite this as:

Piezas, Tito III and Weisstein, Eric W. "Rogers-Ramanujan Continued Fraction." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/Rogers-RamanujanContinuedFraction.html

Subject classifications