An analytic function whose Laurent series
is given by
|
(1)
|
can be integrated term by term using a closed contour encircling
,
|
(2)
| |||
 |
(3)
|
The Cauchy integral theorem requires that the first and last terms vanish, so we have
|
(4)
|
where
is the complex residue. Using the contour
gives
|
(5)
|
so we have
|
(6)
|
If the contour
encloses multiple poles, then the theorem gives the general result
|
(7)
|
where
is the set of poles contained inside the contour. This amazing theorem therefore
says that the value of a contour integral for
any contour in the complex plane depends
only on the properties of a few very special points inside the contour.
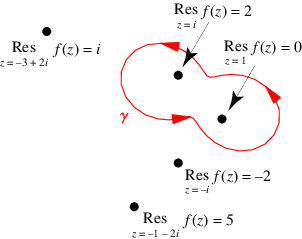
The diagram above shows an example of the residue theorem applied to the illustrated contour and the function
|
(8)
|
Only the poles at 1 and are contained in the contour, which have residues of 0 and
2, respectively. The values of the contour integral
is therefore given by
|
(9)
|