Let
and
be periods of a doubly periodic function,
with
the half-period ratio a number with
. Then Klein's absolute invariant (also called Klein's
modular function) is defined as
|
(1)
|
where
and
are the invariants of the Weierstrass
elliptic function with modular discriminant
|
(2)
|
(Klein 1877). If , where
is the upper half-plane,
then
|
(3)
|
is a function of the ratio only, as are
,
, and
. Furthermore,
,
,
, and
are analytic in
(Apostol 1997, p. 15).
Klein's absolute invariant is implemented in the Wolfram Language as KleinInvariantJ[tau].
The function
is the same as the j-function, modulo a constant
multiplicative factor.
Every rational function of is a modular function,
and every modular function can be expressed as
a rational function of
(Apostol 1997, p. 40).
Klein's invariant can be given explicitly by
![4/(27)([1-lambda(tau)+lambda^2(tau)]^3)/(lambda^2(tau)[1-lambda(tau)]^2)](/images/equations/KleinsAbsoluteInvariant/Inline23.svg) |
(4)
| ||
![([E_4(tau)]^3)/([E_4(tau)]^3-[E_6(tau)^2])](/images/equations/KleinsAbsoluteInvariant/Inline26.svg) |
(5)
|
(Klein 1878-1879, Cohn 1994), where is the elliptic
lambda function
|
(6)
|
is a Jacobi theta function, the
are Eisenstein series,
and
is the nome. Klein's invariant can also be simply expressed
in terms of the five Weber functions
,
,
,
, and
.
is invariant under a unimodular transformation,
so
|
(7)
|
and
is a modular function.
takes on the special values
|
(8)
| |||
|
(9)
| |||
|
(10)
|
satisfies the functional equations
|
(11)
| |||
|
(12)
|
It satisfies a number of beautiful multiple-argument identities, including the duplication formula
|
(13)
| |||
|
(14)
|
with
|
(15)
| |||
|
(16)
|
and
the Dedekind eta function, the triplication
formula
|
(17)
| |||
|
(18)
|
with
|
(19)
| |||
|
(20)
|
and the quintuplication formula
|
(21)
| |||
|
(22)
|
with
|
(23)
| |||
 |
(24)
|
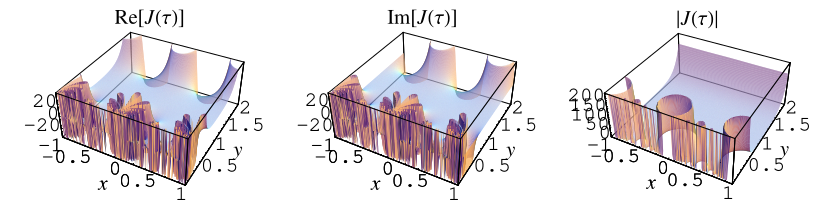
Plotting the real or imaginary part of in the complex plane
produces a beautiful fractal-like structure, illustrated above.