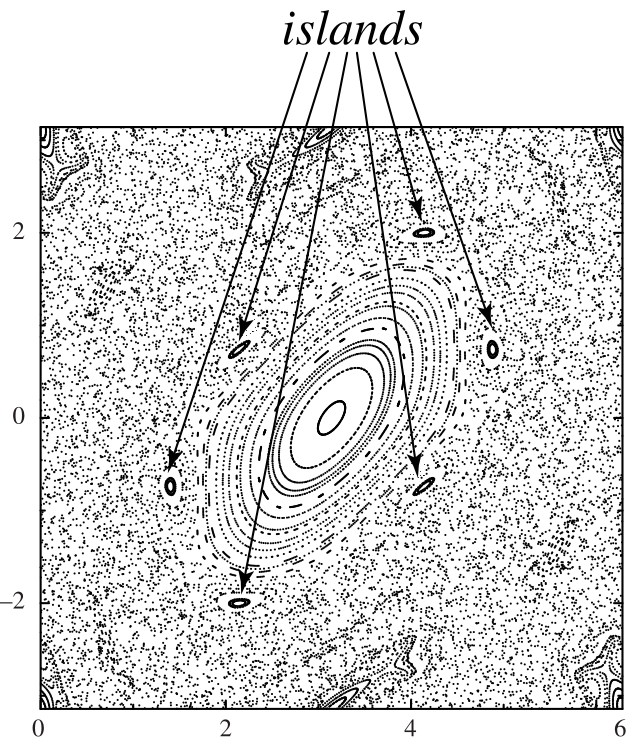
If an integrable quasiperiodic system is slightly perturbed so that it becomes nonintegrable, only a finite number of -map cycles remain as a result of mode
locking. One will be elliptical and one will be hyperbolic.
Surrounding the elliptic fixed point is a region of stable map orbits which circle it, as illustrated
above in the standard map with . As the map is iteratively applied, the island is mapped
to a similar structure surrounding the next point of the elliptic cycle. The map
thus has a chain of islands, with the fixed point
alternating between elliptic (at the center
of the islands) and hyperbolic (between
islands). Because the unperturbed system goes through an infinity
of rational values, the perturbed system must have an infinite
number of island chains.