Consider an arbitrary one-dimensional map
|
(1)
|
(with implicit parameter ) at the onset of chaos. After a
suitable rescaling, the Feigenbaum function
|
(2)
|
is obtained. This function satisfies
|
(3)
|
with .
Proofs for the existence of an even analytic solution to this equation, sometimes called the Feigenbaum-Cvitanović functional equation, have been given by Campanino and Epstein (1981), Campanino et al. (1982), and Lanford (1982, 1984).
The picture above illustrate the Feigenbaum function for
the logistic map with
,
|
(4)
|
along the real axis (M. Trott, pers. comm., Sept. 9, 2003).


The images above show two views of a sculpture presented by Stephen Wolfram to Mitchell Feigenbaum on the occasion of his 60th birthday that depicts the Feigenbaum function
in the complex plane. The sculpture (photos courtesy of A. Young) was designed
by M. Trott and laser-etched into a block of glass by Bathsheba Grossman (http://www.bathsheba.com/). The bottom view
shows
for
approximately between
and 8.
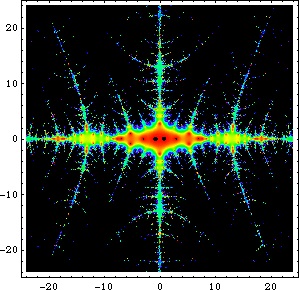
The pictures above illustrate the Feigenbaum function in the complex plane (M. Trott, pers. comm., Sept. 9,
2003).