TOPICS
Search

Epicycloid

DOWNLOAD Mathematica NotebookDownload Wolfram Notebook
EpicycloidDiagram
Epicycloid
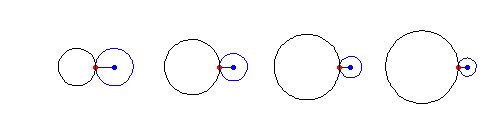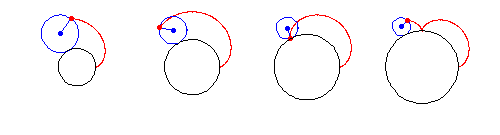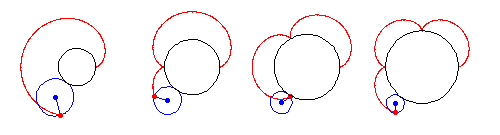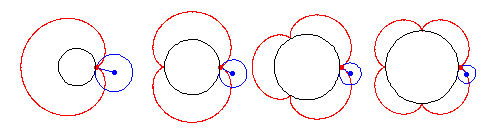
Epicycloid animations

The path traced out by a point P on the edge of a circle of radius b rolling on the outside of a circle of radius a. An epicycloid is therefore an epitrochoid with h=b. Epicycloids are given by the parametric equations

x=(a+b)cosphi-bcos((a+b)/bphi)
(1)
y=(a+b)sinphi-bsin((a+b)/bphi).
(2)

A polar equation can be derived by computing

x^2=(a+b)^2cos^2phi-2b(a+b)cosphicos((a+b)/bphi)+b^2cos^2((a+b)/bphi)
(3)
y^2=(a+b)^2sin^2phi-2b(a+b)sinphisin((a+b)/bphi)+b^2sin^2((a+b)/bphi),
(4)

so

r^2=x^2+y^2=(a+b)^2+b^2-2b(a+b){cos[(a/b+1)phi]cosphi+sin[(a/b+1)phi]sinphi}.
(5)

But

cosalphacosbeta+sinalphasinbeta=cos(alpha-beta),
(6)

so

r^2=(a+b)^2+b^2-2b(a+b)cos[(a/b+1)phi-phi]
(7)
=(a+b)^2+b^2-2b(a+b)cos(a/bphi).
(8)

Note that phi is the parameter here, not the polar angle. The polar angle from the center is

tantheta=y/x=((a+b)sinphi-bsin((a+b)/bphi))/((a+b)cosphi-bcos((a+b)/bphi)).
(9)

To get n cusps in the epicycloid, b=a/n, because then n rotations of b bring the point on the edge back to its starting position.

r^2=a^2[(1+1/n)^2+(1/n)^2-2(1/n)(1+1/n)cos(nphi)]
(10)
=a^2[1+2/n+1/(n^2)+1/(n^2)-(2/n)((n+1)/n)cos(nphi)]
(11)
=a^2[(n^2+2n+2)/(n^2)-(2(n+1))/(n^2)cos(nphi)]
(12)
=(a^2)/(n^2)[(n^2+2n+2)-2(n+1)cos(nphi)],
(13)

so

tantheta=(a((n+1)/n)sinphi-a/nsin[(n+1)phi])/(a((n+1)/n)cosphi-a/ncos[(n+1)phi])
(14)
=((n+1)sinphi-sin[(n+1)phi])/((n+1)cosphi-cos[(n+1)phi]).
(15)

An epicycloid with one cusp is called a cardioid, one with two cusps is called a nephroid, and one with five cusps is called a ranunculoid.

EpicycloidConstruction

Epicycloids can also be constructed by beginning with the diameter of a circle and offsetting one end by a series of steps of equal arc length along the circumference while at the same time offsetting the other end along the circumference by steps n+1 times as large. After traveling around the circle once, the envelope of an n-cusped epicycloid is produced, as illustrated above (Madachy 1979).

Epicycloids have torsion

tau=0
(16)

and satisfy

(s^2)/(a^2)+(rho^2)/(b^2)=1,
(17)

where rho is the radius of curvature (1/kappa).

See also

Cardioid, Cyclide, Cycloid, Epicycloid Evolute, Epicycloid Involute, Epicycloid Pedal Curve, Epitrochoid, Hypocycloid, Nephroid, Ranunculoid

Explore with Wolfram|Alpha

References

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 217, 1987.Bogomolny, A. "Cycloids." http://www.cut-the-knot.org/pythagoras/cycloids.shtml.Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 160-164 and 169, 1972.Lemaire, J. Hypocycloïdes et epicycloïdes. Paris: Albert Blanchard, 1967.MacTutor History of Mathematics Archive. "Epicycloid." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Epicycloid.html.Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 219-225, 1979.Smith, D. E. History of Mathematics, Vol. 2: Special Topics of Elementary Mathematics. New York: Dover, p. 328, 1958.Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 50-52, 1991.Yates, R. C. "Epi- and Hypo-Cycloids." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 81-85, 1952.

Cite this as:

Weisstein, Eric W. "Epicycloid." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/Epicycloid.html

Subject classifications