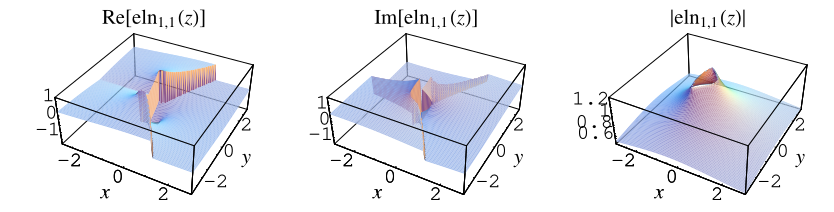
The elliptic logarithm is generalization of integrals of the form
for
real, which can be expressed in terms of logarithmic and inverse trigonometric functions,
to
for
and
real. This integral can be done analytically, but has a complicated form involving
incomplete elliptic integrals of the first kind with complex parameters. The plots
above show the special case
.
The elliptic logarithm is implemented in the Wolfram Language as EllipticLog[x, y
,
a, b
], where
is an unfortunate and superfluous parameter that must be set
to either
or
and which multiplies the above integral by a factor of
.
The inverse of the elliptic logarithm is the elliptic exponential function.