The disdyakis triacontahedron is the dual polyhedron of the Archimedean great rhombicosidodecahedron. It is also known as the hexakis icosahedron (Holden 1971, p. 55). It is illustrated above together with a wireframe version and a net that can be used for its construction.
It is Wenninger dual .
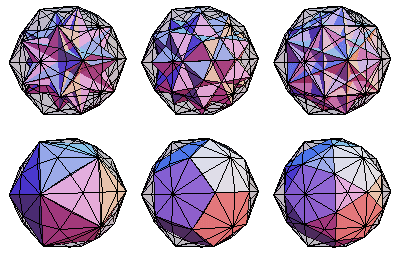
A tetrahedron 10-compound, octahedron 5-compound, cube 5-compound, icosahedron, dodecahedron, and icosidodecahedron can be inscribed in the vertices of a disdyakis triacontahedron (E. Weisstein, Dec. 26-27, 2009).
Starting with an Archimedean great rhombicosidodecahedron of unit edge lengths, the edge lengths of the corresponding disdyakis triacontahedron are
|
(1)
| |||
 |
(2)
| ||
 |
(3)
|
The corresponding midradius is
 |
(4)
|
The surface area and volume are
|
(5)
| |||
|
(6)
|
