The velocity vector of a particle is the time derivative of its position vector. The notion comes from classical
physics. By representing the position and motion of a single particle using vectors,
the equations for motion are simpler and more intuitive. Suppose the position of
a particle at time 
is given by the position vector 
. Then the velocity vector 
is the derivative of the
position,
 |
For example, suppose a particle is confined to the plane and its position is given by 
. Then it travels along the unit
circle at constant speed. Its velocity vector is 
. In a diagram, it makes
sense to translate the velocity vector so it originates
at 
.
In particular, it is drawn as an arrow from 
to 
.
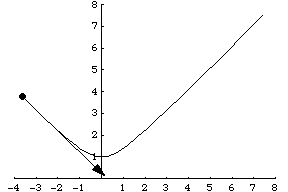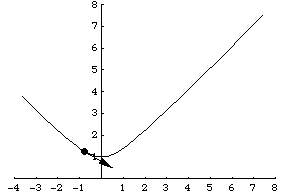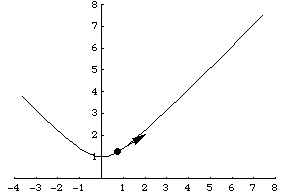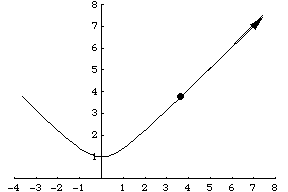
Another example is a particle traveling along a hyperbola specified parametrically by 
. Its velocity vector is then given by
, illustrated above.
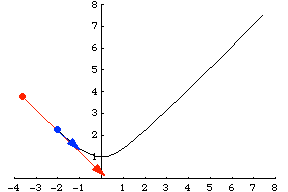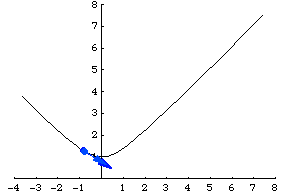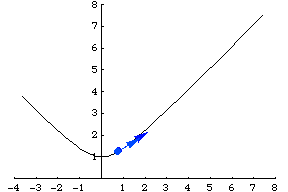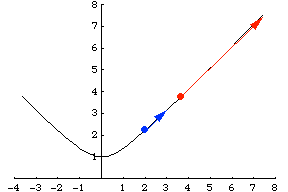
Traveling down the same path using a different function is called a reparameterization, and the chain rule describes the change in velocity. For example,
the hyperbola can also be parametrized by 
. Note that 
, and by the chain
rule, 
.
Note that the set of possible velocity vectors forms a vector space. If 
and 
are two paths through the origin,
then so is 
and the velocity vector of this path is 
. Similarly, if 
is a scalar, then the path 
has velocity vector 
. It makes sense to distinguish the velocity vectors at
different points. In physics, phase
space consists of position and momentum variables. A metric
and a specified mass can identify velocities with momenta in elementary particle
mechanics. In mathematics, the velocity vectors form the tangent
space, and the collection of tangent spaces
forms the tangent bundle.
