Sphere Point Picking

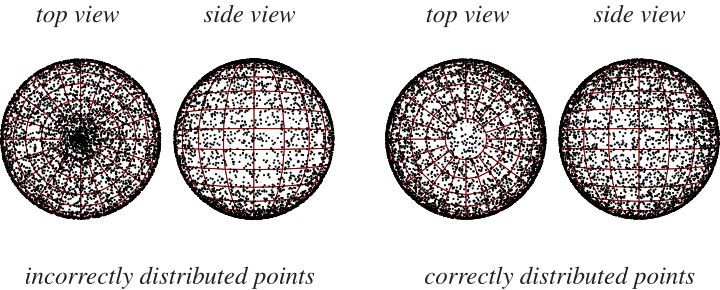
To pick a random point on the surface of a unit sphere, it is incorrect to select spherical coordinates and from uniform distributions and , since the area element is a function of , and hence points picked in this way will be "bunched" near the poles (left figure above).

random points can be picked on a unit sphere in the Wolfram Language using the function RandomPoint[Sphere[], n].

To obtain points such that any small area on the sphere is expected to contain the same number of points (right figure above), choose and to be random variates on . Then

			(1)
			(2)

gives the spherical coordinates for a set of points which are uniformly distributed over . This works since the differential element of solid angle is given by

(3)

The distribution of polar angles can be found from

(4)

by taking the derivative of (2) with respect to to get , solving (2) for , and plugging the results back in to (4) with to obtain the distribution

(5)

Similarly, we can pick to be uniformly distributed (so we have ) and obtain the points

			(6)
			(7)
			(8)

with and , which are also uniformly distributed over .

Marsaglia (1972) derived an elegant method that consists of picking and from independent uniform distributions on and rejecting points for which . From the remaining points,

			(9)
			(10)
			(11)

have a uniform distribution on the surface of a unit sphere. This method can also be extended to hypersphere point picking. The plots above show the distribution of points for 100, 1000, and 5000 initial points (where the counts refer to the number of points before throwing away).

Cook (1957) extended a method of von Neumann (1951) to give a simple method of picking points uniformly distributed on the surface of a unit sphere. Pick four numbers , , , and from a uniform distribution on , and reject pairs with

(12)

From the remaining points, the rules of quaternion transformation then imply that the points with Cartesian coordinates

			(13)
			(14)
			(15)

have the desired distribution (Cook 1957, Marsaglia 1972). The plots above show the distribution of points for 100, 1000, and 5000 initial points (where the counts refers to the number of points before throwing away).

Another easy way to pick a random point on a sphere is to generate three Gaussian random variables , , and . Then the distribution of the vectors

(16)

is uniform over the surface (Muller 1959, Marsaglia 1972).