The th roots of unity are roots
of the cyclotomic
equation
which are known as the de Moivre numbers. The notations ,
, and
, where the value of
is understood by context, are variously used to denote the
th
th root of unity.
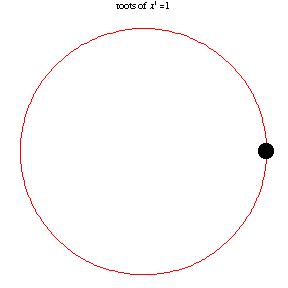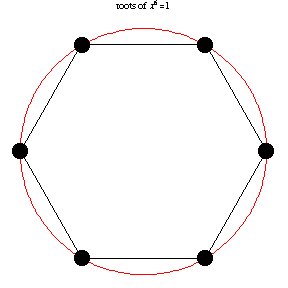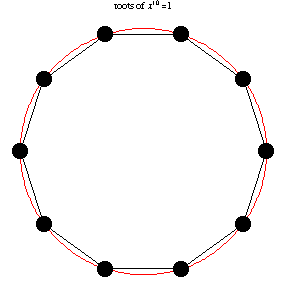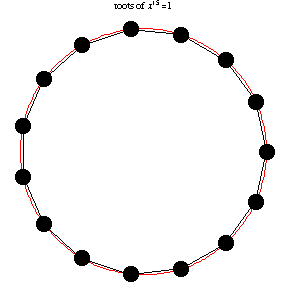
is always an
th root of unity, but
is such a root only if
is even. In general, the roots of unity form a regular
polygon with
sides, and each vertex lies on the unit circle.