has decimal expansion given by
 |
(1)
|
(OEIS A000796). The following table summarizes some record computations of the digits of 
.
 | 1999 | Kanada, Ushio and Kuroda |
 | Dec. 2002 | Kanada, Ushio and Kuroda (Peterson 2002, Kanada 2003) |
 | Aug. 2012 | A. J. Yee (Yee) |
 | Aug. 2012 | S. Kondo and A. J. Yee (Yee) |
 | Dec. 2013 | A. J. Yee and S. Kondo (Yee) |
The calculation of the digits of 
has occupied mathematicians since the day of the Rhind papyrus
(1500 BC). Ludolph van Ceulen spent much of his life calculating 
to 35 places. Although he did not live to publish his result,
it was inscribed on his gravestone. Wells (1986, p. 48) discusses a number of
other calculations. The calculation of 
also figures in the Season 2 Star
Trek episode "Wolf
in the Fold" (1967), in which Captain Kirk and Mr. Spock force an evil
entity (composed of pure energy and which feeds on fear) out of the starship Enterprise's
computer by commanding the computer to "compute to the last digit the value
of pi," thus sending the computer into an infinite loop.
Al-Kāshi of Samarkand computed the sexagesimal digits of 
as
 |
(2)
|
(OEIS A091649) using 
-gons, a value accurate to 17 decimal places (Borwein
and Bailey 2003, p. 107).
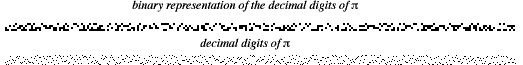
The binary representation of the decimal digits of 
(top figure) and decimal representation (bottom figure) of
are illustrated above.
A plot of the first 1600 decimal digits of 
(mod 2) is shown above (left figure), with the corresponding
plot for 22/7 shown at right. Here, white indicates an even digit and black an odd
digit (Pickover 2002, p. 285).
Spigot (Rabinowitz and Wagon 1995; Arndt and Haenel 2001; Borwein and Bailey 2003, pp. 140-141) and base-16 digit-extraction
algorithms (the BBP formula) are known for 
. A remarkable recursive formula conjectured
to give the 
th
hexadecimal digit of 
is given by 
, where 
is the floor function,
 |
(3)
|
is the fractional
part and 
(Borwein and Bailey 2003, Ch. 4; Bailey et al. 2007, pp. 22-23).
The limit pi formulas
 |
(4)
|
and
 |
(5)
|
where 
is a Bernoulli
number (Plouffe 2022) can be used as a digit-extraction
algorithm for 
(as well as 
).
In particular, letting
 |
(6)
|
the 
th digit to the right of the decimal point
of 
for 
is given by
 |
(7)
|
where 
is the integer
part and 
is the fractional part. Similar formulas can be
obtained using
 |
(8)
|
and
 |
(9)
|
where 
is an Euler
number, which gives a base-9 (or binary) digit-extraction
algorithm (Plouffe 2022). Related limits and formulas can also be obtained for
(Plouffe 2022).
Pi-primes, i.e., 
-constant primes occur
at 2, 6, 38, 16208, 47577, 78073, 613373, ... (OEIS A060421)
decimal digits.
The beast number 666 appears in 
at decimals 2440, 3151, 4000, 4435, 5403, 6840, (OEIS A083625). The first occurrences of just 
consecutive 6s are 7, 117, 2440, 21880, 48439, 252499, 8209165,
55616210, 45681781, ... (OEIS A096760), while
(or more) consecutive 6s first occur
at 7, 117, 2440, 21880, 48439, 252499, 8209165, 45681781, 45681781, ... (OEIS A050285).
The digits 314159 appear at positions 176451, 1259351, 1761051, 6467324, 6518294, 9753731, 9973760, ... (correcting Pickover 1995).
The sequence 0123456789 occurs beginning at digits 
, 
, 
, 
, 
, and 
(OEIS A101815;
cf. Wells 1986, pp. 51-52).
The sequence 9876543210 occurs beginning at digits 
, 
, 
, 
, and 
(OEIS A101816).
The sequence 27182818284 (the first few digits of e) occurs beginning at digit 
(see also Pickover's sequence).
There are also interesting patterns for 
. 0123456789 occurs at 
, 9876543210 occurs at 
and 
, and 999999999999 occurs at 
of 
.
The starting positions of the first occurrence of 
, 1, 2, ... in the decimal expansion of 
(including the initial 3 and counting it as the first digit)
are 33, 2, 7, 1, 3, 5, 8, 14, ... (OEIS A032445).
Scanning the decimal expansion of 
until all 
-digit numbers have occurred, the last 1-, 2-, ... digit numbers
appearing are 0, 68, 483, 6716, 33394, 569540, ... (OEIS A032510),
which end at digits 33, 607, 8556, 99850, 1369565, ... (OEIS A080597).
A curiosity relating 
to the beast number 666 involves adding the first
three sextads of 
.
First, note that
 |
(10)
|
Now, skip ahead 15 decimal places and note that the sum is repeated as
 |
(11)
|
(pers. comm., P. Olivera, Aug. 11, 2005; Olivera).
It is not known if 
is normal (Wagon 1985, Bailey and Crandall 2001),
although the first 30 million digits are very uniformly
distributed (Bailey 1988).
The following distribution of decimal digits 
is found for the first 
digits of 
(Kanada 2003). It shows no statistically significant
departure from a uniform distribution.
 | OEIS | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 0 | A099291 | 8 | 93 | 968 | 9999 | 99959 | 999440 | 9999922 | 99993942 | 999967995 | 10000104750 | 99999485134 |
| 1 | A099292 | 8 | 116 | 1026 | 10137 | 99758 | 999333 | 10002475 | 99997334 | 1000037790 | 9999937631 | 99999945664 |
| 2 | A099293 | 12 | 103 | 1021 | 9908 | 100026 | 1000306 | 10001092 | 100002410 | 1000017271 | 10000026432 | 100000480057 |
| 3 | A099294 | 11 | 102 | 974 | 10025 | 100229 | 999964 | 9998442 | 99986911 | 999976483 | 9999912396 | 99999787805 |
| 4 | A099295 | 10 | 93 | 1012 | 9971 | 100230 | 1001093 | 10003863 | 100011958 | 999937688 | 10000032702 | 100000357857 |
| 5 | A099296 | 8 | 97 | 1046 | 10026 | 100359 | 1000466 | 9993478 | 99998885 | 1000007928 | 9999963661 | 99999671008 |
| 6 | A099297 | 9 | 94 | 1021 | 10029 | 99548 | 999337 | 9999417 | 100010387 | 999985731 | 9999824088 | 99999807503 |
| 7 | A099298 | 8 | 95 | 970 | 10025 | 99800 | 1000207 | 9999610 | 99996061 | 1000041330 | 10000084530 | 99999818723 |
| 8 | A099299 | 12 | 101 | 948 | 9978 | 99985 | 999814 | 10002180 | 100001839 | 999991772 | 10000157175 | 100000791469 |
| 9 | A099300 | 14 | 106 | 1014 | 9902 | 100106 | 1000040 | 9999521 | 100000273 | 1000036012 | 9999956635 | 99999854780 |
The following table gives the first few positions at which a digit 
occurs 
times. The sequence 1, 135, 1698, 54525, 24466, 252499, 3346228,
46663520, 564665206, ... (OEIS A061073) given
by the diagonal (plus any terms of the form 10 10's etc.) is known as the Earls
sequence (Pickover 2002, p. 339). The sequence 999999 occurs at decimal
762 (which is sometimes called the Feynman point;
Wells 1986, p. 51) and continues as 9999998, which is largest value of any seven
digits in the first million decimals.
 | OEIS | strings of
1, 2, ... s
first occur at |
| 0 | A050279 | 32, 307, 601, 13390, 17534, 1699927, ... |
| 1 | A035117 | 1, 94, 153, 12700, 32788, 255945, ... |
| 2 | A050281 | 6, 135, 1735, 4902, 65260, 963024, ... |
| 3 | A050282 | 9, 24, 1698, 28467, 28467, 710100, ... |
| 4 | A050283 | 2, 59, 2707, 54525, 808650, 828499, ... |
| 5 | A050284 | 4, 130, 177, 24466, 24466, 244453, ... |
| 6 | A050285 | 7, 117, 2440, 21880, 48439, 252499, ... |
| 7 | A050286 | 13, 559, 1589, 1589, 162248, 399579, ... |
| 8 | A050287 | 11, 34, 4751, 4751, 213245, 222299, ... |
| 9 | A048940 | 5, 44, 762, 762, 762, 762, 1722776, ... |
Knuth (2024, p. 18) notes a "miraculous" occurrence of the first 30 digits of 
in the graceful pi-way, namely a particular graceful labeling of the contiguous
USA graph.
." Amer. Math. Monthly 104,
852-855, 1997.Anderson, D. "The Pi-Search Page." 
to 
Decimal Digit using Borwein's'
Quartically Convergent Algorithm." Math. Comput. 50, 283-296,
1988.Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn,
R.; Luke, D. R.; and Moll, V. H. 
." 
'th
Decimal Digit or Binary of 
and 
." 
."
Amer. Math. Monthly 102, 195-203, 1995.Sloane, N. J. A.
Sequences 
Normal?" Math. Intel. 7, 65-67, 1985.Wells, D. 
." Math. Teacher 53, 644-650, 1960.Yee,
A. J. "y-cruncher - A Multi-Threaded Pi-Program."