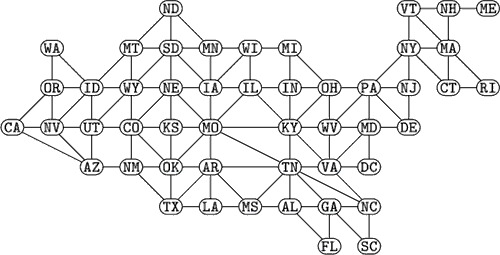
The "contiguous USA graph" is the graph whose vertices represent the contiguous 48 states of the United States plus the District of Columbia (DC) and whose edges connect pairs of states (plus DC) that are connected by at least one drivable road (Knuth 2008, p. 15).
The Contiguous USA graph is implemented in the Wolfram Language as GraphData["ContiguousUSAGraph"].
This graph has 49 vertices and 107 edges. It is a planar, bridged (the only bridge being the edge between New Hampshire and Maine), identity graph and is nonhamiltonian but traceable.
Two related geographic graphs are the 13 colonies graph and the Wagon USA map graph. The 13 colonies graph is the induced subgraph on the present-day states corresponding to the original colonies. The Wagon USA map graph is obtained by removing DC and adding vertices for Lake Michigan and the entire exterior region, together with their region-adjacency edges.
The following table lists the states by vertex degree (i.e., number of other states to which they're connected).
 | states |
| 1 | ME |
| 2 | DC, FL, RI, SC, WA |
| 3 | CA, CT, DE, LA, MI, ND, NH, NJ, VT |
| 4 | AL, AZ, IN, KS, MN, MS, MT, NC, NM, OR, TX, WI |
| 5 | GA, IL, MA, MD, NV, NY, OH, UT, WV |
| 6 | AR, CO, IA, ID, NE, OK, PA, SD, VA, WY |
| 7 | KY |
| 8 | MO, TN |
The contiguous USA graph has chromatic number 4 and fractional chromatic number 7/2, with corresponding minimal colorings illustrated above (S. Wagon, pers. comm., Dec. 8, 2011).
Rather amazingly, the contiguous USA graph is graceful, as illustrated above. More amazingly still, T. Rokicki found in October 2020 that the graceful labeling illustrated above labels the 15 states on the western and northern borders from California to Maine with the numbers 31, 41, 59, 26, 53, 58, 97, 93, 23, 84, 62, 64, 33, 83, and 27, precisely the first 30 decimal digits of pi. Knuth (2025, p. 18) describes this as a "graceful miracle." With apologies to Gordon Lightfoot's "Carefree Highway," the path shown in red might be termed the "graceful pi-way."
