|
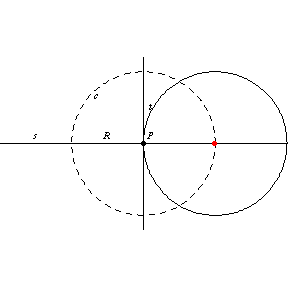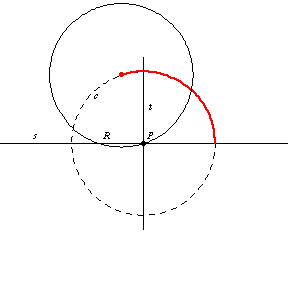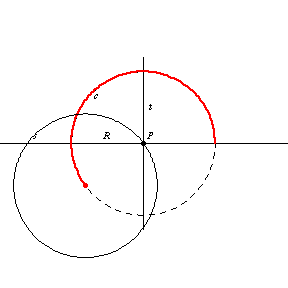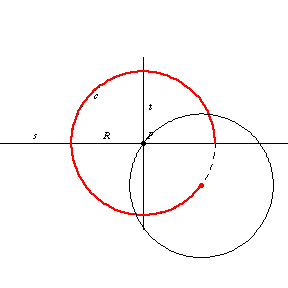
|
According to G. Pólya, the method of finding geometric objects by intersection.
1. For example, the centers of all circles tangent to a straight line at a given point
lie on a line
that passes through
and is perpendicular to
.
2. In addition, the circle centered at
with radius
is the locus of the centers of all circles of radius
passing through
.
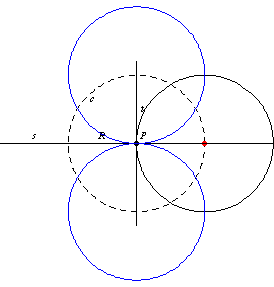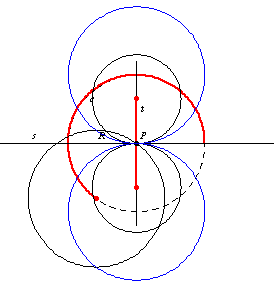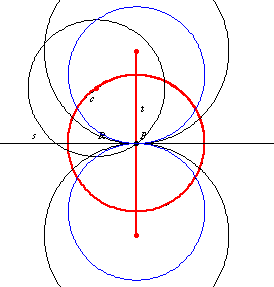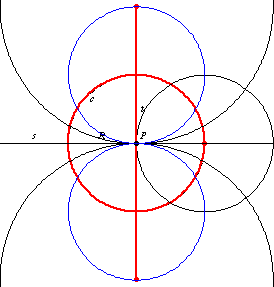
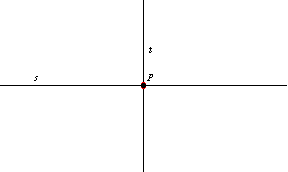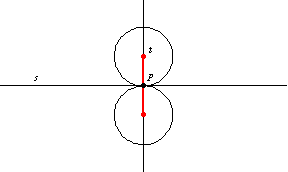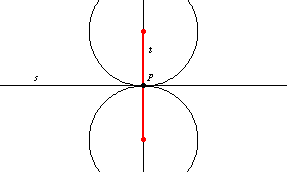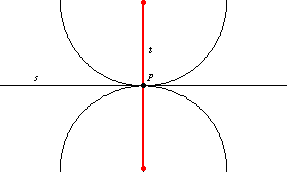
The intersection of
and
consists of two points
and
which are the centers of two circles of radius
tangent to
at
.
Many constructions with straightedge and compass are based on this method, as, for example, the construction of the center of a given circle by means of the perpendicular bisector theorem.