The limaçon trisectrix is a trisectrix that is a special case of the rose curve with (possibly with translation, rotation, and scaling). It
was studied by Archimedes, as well as by Étienne Pascal in 1630.
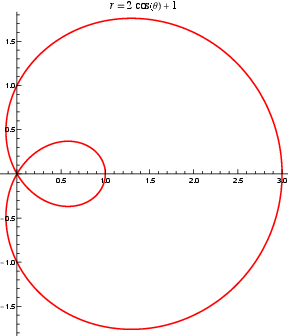
In its most commonly written standard form, the limaçon trisectrix has polar equation
|
(1)
|
(Ferréol). It can be expressed as the Cartesian equation
|
(2)
|
or
|
(3)
|
The limaçon trisectrix is the cardioid pedal curve with respect to the center of its conchoidal circle (Ferréol).
It has arc length
 |
(4)
|
where
is a complete elliptic integral
of the second kind. Its outer boundary encloses an area
|
(5)
|
and its inner lopp has area
|
(6)
|
As a special case of the rose curve , the polar equation
is given by
|
(7)
|
which must be rotated by , scaled by a factor of 2, shifted by distance 1 to
the right, and plotted from
to
to obtain the curve in its standard form.