Lemon Surface

A surface of revolution defined by Kepler. It consists of less than half of a circular arc rotated about an axis passing through the endpoints of the arc. The equations of the upper and lower boundaries in the plane are

(1)

for and . The cross section of a lemon is a lens. The lemon is the inside surface of a spindle torus. The American football is shaped like a lemon.

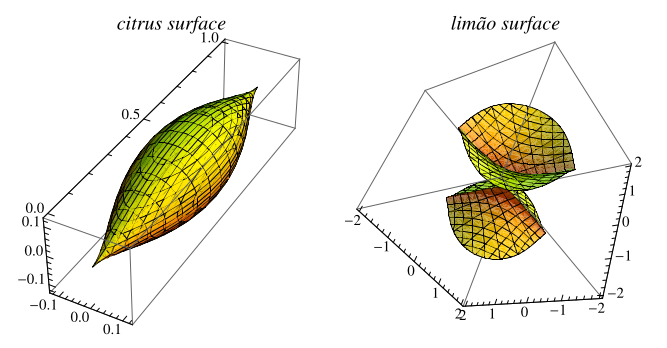
Two other lemon-shaped surfaces are given by the sextic surface

(2)

called the "citrus" (or zitrus) surface by Hauser (left figure), and the sextic surface

(3)

whose upper and lower portions resemble two halves of a lemon, called the limão surface by Hauser (right figure).

The citrus surface had bounding box , centroid at , volume

(4)

and a moment of inertia tensor

(5)

for a uniform density solid citrus with mass .