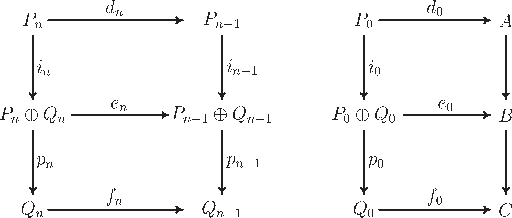
Given a short exact sequence of modules
|
(1)
|
let
|
(2)
|
|
(3)
|
be projective resolutions of and
, respectively. Then there is a projective resolution of
|
(4)
|
such that the above diagrams are commutative. Here,
is the injection of the first summand, whereas
is the projection onto the second
factor for
.
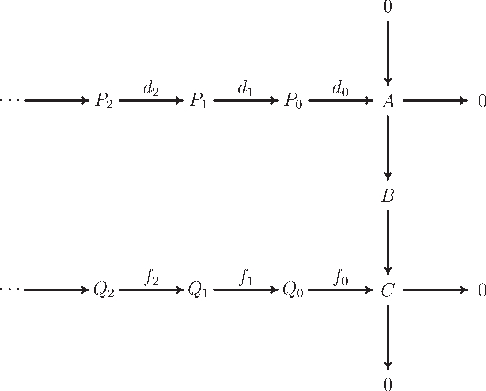
The name of this lemma derives from the shape of the diagram formed by the short exact sequence and the given projective resolutions.