In the moving sofa problem, naming finding the plane figure ("sofa") of largest area that can be moved around a right-angled corner in a two-dimensional
hallway of unit width, Hammersley (Croft et al. 1994, Rommik) found a shape
with area larger than that of a half-disk by cutting the half-disk into two quarter-disks,
separating them horizontally by a distance
while filling in the gap between them. Additionally, a smaller
half-disk of radius
is removed from the bottom, as illustrated above.
The resulting "Hammersley sofa" is illustrated above for various values of ,
changing shape from a half-disk at
to a shape whose two halves meet at a single point at
.
The Hammersley sofa has area
|
(1)
|
and perimeter
|
(2)
|
which, as expected, reduce to the values for the half disk and
as
. A plot of
as a function of
from
to
is shown above.
is maximized when
, giving an area
|
(3)
|
(OEIS A086118; Croft et al. 1994, Rommik).
The maximal Hammersley sofa is illustrated above.
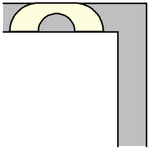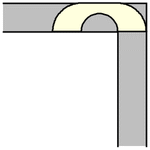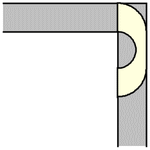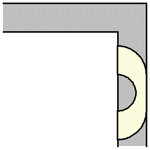
As it turns out, the Hammersley sofa can move around the corner for any value , including the radius
giving a maximum area. The process
is illustrated above for the maximal Hammersley sofa (Romik 2016).
A slightly larger sofa, now known as the Gerver sofa, was subsequently found and eventually proved to be optimal.