Gerver Sofa

Gerver (1992) found a sofa with larger area than that of the optimal Hammersley sofa that solves the moving sofa problem. Gerver also provided arguments indicating that it is either optimal or close to it. The boundary of Gerver's sofa is a complicated shape composed of 3 straight line segments and 15 curved pieces, each of which is described by an analytic expression. It is illustrated above (Romik 2016, 2018).

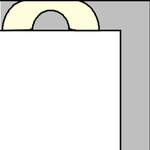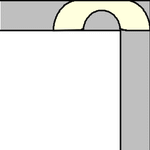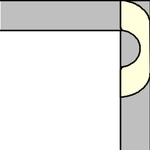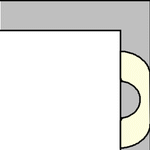
An animation of the Gerver sofa rounding the turn is shown above (Romik 2016).

The area of the Gerver sofa can be given by defining the constants , , , and by solving

	(1)
	(2)
	(3)
	(4)

(Gerver 1992, Finch 2003). This gives

			(5)
			(6)
			(7)
			(8)

(Gerver 1992, Finch 2003).

Now define

(9)

where

			(10)
			(11)
			(12)
			(13)

(Gerver 1992, Finch 2003).

Finally, define the functions

			(14)
			(15)
			(16)

The area of the optimal sofa is then given by

			(17)
			(18)

(OEIS A128463; Gerver 1992, Finch 2003), a value slightly larger than the area of 2.207416 (OEIS A086118) for the maximal Hammersley sofa and which can be called the moving sofa constant.

Assuming convex trajectories and envelopes, Deng (2024) used the calculus of variations to formulate an integral functional on a set of parametric equations for curves that determined the sofa shape by solving the Euler-Lagrange differential equations Using numerical methods, this gave a shape with area 2.2195316, consistent with Gerver's sofa. Baek (2024) showed that Gerver's construction attains the maximum area 2.2195...using a proof does not require computer assistance except for numerical computations that can be done on a scientific calculator.